Advertisements
Advertisements
Question
Suppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point, a distance h directly above the tunnel. The motion of the particle as seen from the earth is
(a) simple harmonic
(b) parabolic
(c) on a straight line
(d) periodic
Solution
(c) on a straight line
(d) periodic
If the particle were dropped from the surface of the earth, the motion of the particle would be SHM. But when it is dropped from a height h, the motion of the particle is not SHM because there is no horizontal velocity imparted. In that case, the motion of the particle would be periodic and in a straight line.
APPEARS IN
RELATED QUESTIONS
In measuring time period of a pendulum, it is advised to measure the time between consecutive passage through the mean position in the same direction. This is said to result in better accuracy than measuring time between consecutive passage through an extreme position. Explain.
The energy of system in simple harmonic motion is given by \[E = \frac{1}{2}m \omega^2 A^2 .\] Which of the following two statements is more appropriate?
(A) The energy is increased because the amplitude is increased.
(B) The amplitude is increased because the energy is increased.
The distance moved by a particle in simple harmonic motion in one time period is
The average energy in one time period in simple harmonic motion is
A pendulum clock that keeps correct time on the earth is taken to the moon. It will run
A pendulum clock keeping correct time is taken to high altitudes,
A pendulum clock keeping correct time is taken to high altitudes,
A particle moves in a circular path with a continuously increasing speed. Its motion is
In a simple harmonic motion
Which of the following will change the time period as they are taken to moon?
(a) A simple pendulum
(b) A physical pendulum
(c) A torsional pendulum
(d) A spring-mass system
A simple pendulum of length 40 cm is taken inside a deep mine. Assume for the time being that the mine is 1600 km deep. Calculate the time period of the pendulum there. Radius of the earth = 6400 km.
A particle is subjected to two simple harmonic motions given by x1 = 2.0 sin (100π t) and x2 = 2.0 sin (120 π t + π/3), where x is in centimeter and t in second. Find the displacement of the particle at (a) t = 0.0125, (b) t = 0.025.
A particle is subjected to two simple harmonic motions, one along the X-axis and the other on a line making an angle of 45° with the X-axis. The two motions are given by x = x0 sin ωt and s = s0 sin ωt. Find the amplitude of the resultant motion.
If the inertial mass and gravitational mass of the simple pendulum of length l are not equal, then the time period of the simple pendulum is
Define the frequency of simple harmonic motion.
What is an epoch?
A body oscillates with SHM according to the equation x = 5 cos `(2π"t" + π/4)`. Its instantaneous displacement at t = 1 sec is:
The displacement of a particle is represented by the equation y = sin3ωt. The motion is ______.
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
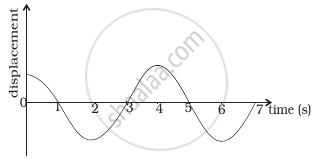
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
Assume there are two identical simple pendulum clocks. Clock - 1 is placed on the earth and Clock - 2 is placed on a space station located at a height h above the earth's surface. Clock - 1 and Clock - 2 operate at time periods 4 s and 6 s respectively. Then the value of h is ______.
(consider the radius of earth RE = 6400 km and g on earth 10 m/s2)
