Advertisements
Advertisements
Question
A particle moves on the X-axis according to the equation x = A + B sin ωt. The motion is simple harmonic with amplitude
Options
A
B
A + B
\[\sqrt{A^2 + B^2} .\]
Solution
B
At t = 0,
Displacement \[\left( x_0 \right)\] is given by, x0 = A + sin ω(0) = A
Displacement x will be maximum when sinωt is 1 or,
xm = A + B
Amplitude will be:
xm \[-\]xo = A + B \[-\] A = B
APPEARS IN
RELATED QUESTIONS
The average displacement over a period of S.H.M. is ______.
(A = amplitude of S.H.M.)
State the differential equation of linear simple harmonic motion.
The energy of system in simple harmonic motion is given by \[E = \frac{1}{2}m \omega^2 A^2 .\] Which of the following two statements is more appropriate?
(A) The energy is increased because the amplitude is increased.
(B) The amplitude is increased because the energy is increased.
Can a pendulum clock be used in an earth-satellite?
A platoon of soldiers marches on a road in steps according to the sound of a marching band. The band is stopped and the soldiers are ordered to break the steps while crossing a bridge. Why?
The time period of a particle in simple harmonic motion is equal to the smallest time between the particle acquiring a particular velocity \[\vec{v}\] . The value of v is
The displacement of a particle is given by \[\overrightarrow{r} = A\left( \overrightarrow{i} \cos\omega t + \overrightarrow{j} \sin\omega t \right) .\] The motion of the particle is
A pendulum clock that keeps correct time on the earth is taken to the moon. It will run
The motion of a torsional pendulum is
(a) periodic
(b) oscillatory
(c) simple harmonic
(d) angular simple harmonic
A particle moves on the X-axis according to the equation x = x0 sin2 ωt. The motion is simple harmonic
In a simple harmonic motion
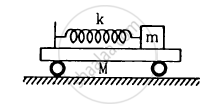
All the surfaces shown in figure are frictionless. The mass of the care is M, that of the block is m and the spring has spring constant k. Initially the car and the block are at rest and the spring is stretched through a length x0 when the system is released. (a) Find the amplitudes of the simple harmonic motion of the block and of the care as seen from the road. (b) Find the time period(s) of the two simple harmonic motions.
A spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
Assume that a tunnel is dug across the earth (radius = R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of \[\sqrt{gR}\] (b) it is released from a height R above the tunnel (c) it is thrown vertically upward along the length of tunnel with a speed of \[\sqrt{gR}\]
A closed circular wire hung on a nail in a wall undergoes small oscillations of amplitude 20 and time period 2 s. Find (a) the radius of the circular wire, (b) the speed of the particle farthest away from the point of suspension as it goes through its mean position, (c) the acceleration of this particle as it goes through its mean position and (d) the acceleration of this particle when it is at an extreme position. Take g = π2 m/s2.
A uniform disc of mass m and radius r is suspended through a wire attached to its centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
A simple pendulum is suspended from the roof of a school bus which moves in a horizontal direction with an acceleration a, then the time period is
The displacement of a particle varies with time according to the relation y = a sin ωt + b cos ωt.
A container consist of hemispherical shell of radius 'r ' and cylindrical shell of height 'h' radius of same material and thickness. The maximum value h/r so that container remain stable equilibrium in the position shown (neglect friction) is ______.

Assume there are two identical simple pendulum clocks. Clock - 1 is placed on the earth and Clock - 2 is placed on a space station located at a height h above the earth's surface. Clock - 1 and Clock - 2 operate at time periods 4 s and 6 s respectively. Then the value of h is ______.
(consider the radius of earth RE = 6400 km and g on earth 10 m/s2)
