Advertisements
Advertisements
Question
State the laws of the simple pendulum?
Solution
- Law of length: For a given value of acceleration due to gravity, the time period of a simple pendulum is directly proportional to the square root of the length of the pendulum.
`"T" ∝ sqrt"l"` - Law of acceleration: For a fixed length, the time period of a simple pendulum is inversely proportional to the square root of acceleration due to gravity.
`"T" ∝ 1/sqrt"g"` - The period of a simple pendulum is independent of its mass.
- A simple pendulum's period is independent of its amplitude (for small amplitudes).
APPEARS IN
RELATED QUESTIONS
Assuming the expression for displacement of a particle starting from extreme position, explain graphically the variation of velocity and acceleration w.r.t. time.
The time period of a particle in simple harmonic motion is equal to the time between consecutive appearances of the particle at a particular point in its motion. This point is
The displacement of a particle in simple harmonic motion in one time period is
A pendulum clock that keeps correct time on the earth is taken to the moon. It will run
The motion of a torsional pendulum is
(a) periodic
(b) oscillatory
(c) simple harmonic
(d) angular simple harmonic
A small block oscillates back and forth on a smooth concave surface of radius R ib Figure . Find the time period of small oscillation.
Assume that a tunnel is dug across the earth (radius = R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of \[\sqrt{gR}\] (b) it is released from a height R above the tunnel (c) it is thrown vertically upward along the length of tunnel with a speed of \[\sqrt{gR}\]
A body oscillates with SHM according to the equation x = 5 cos `(2π"t" + π/4)`. Its instantaneous displacement at t = 1 sec is:
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
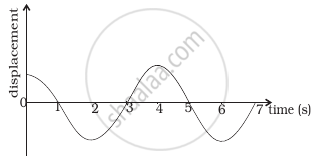
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
Assume there are two identical simple pendulum clocks. Clock - 1 is placed on the earth and Clock - 2 is placed on a space station located at a height h above the earth's surface. Clock - 1 and Clock - 2 operate at time periods 4 s and 6 s respectively. Then the value of h is ______.
(consider the radius of earth RE = 6400 km and g on earth 10 m/s2)
