Advertisements
Advertisements
Question
A particle executes simple harmonic motion. If you are told that its velocity at this instant is zero, can you say what is its displacement? If you are told that its velocity at this instant is maximum, can you say what is its displacement?
Solution
No, we cannot say anything from the given information. To determine the displacement of the particle using its velocity at any instant, its mean position has to be known.
APPEARS IN
RELATED QUESTIONS
A particle in S.H.M. has a period of 2 seconds and amplitude of 10 cm. Calculate the acceleration when it is at 4 cm from its positive extreme position.
State the differential equation of linear simple harmonic motion.
A particle executes simple harmonic motion Let P be a point near the mean position and Q be a point near an extreme. The speed of the particle at P is larger than the speed at Q. Still the particle crosses Pand Q equal number of times in a given time interval. Does it make you unhappy?
It is proposed to move a particle in simple harmonic motion on a rough horizontal surface by applying an external force along the line of motion. Sketch the graph of the applied force against the position of the particle. Note that the applied force has two values for a given position depending on whether the particle is moving in positive or negative direction.
A pendulum clock gives correct time at the equator. Will it gain time or loose time as it is taken to the poles?
A platoon of soldiers marches on a road in steps according to the sound of a marching band. The band is stopped and the soldiers are ordered to break the steps while crossing a bridge. Why?
The force acting on a particle moving along X-axis is F = −k(x − vo t) where k is a positive constant. An observer moving at a constant velocity v0 along the X-axis looks at the particle. What kind of motion does he find for the particle?
The distance moved by a particle in simple harmonic motion in one time period is
The displacement of a particle is given by \[\overrightarrow{r} = A\left( \overrightarrow{i} \cos\omega t + \overrightarrow{j} \sin\omega t \right) .\] The motion of the particle is
Which of the following quantities are always positive in a simple harmonic motion?
For a particle executing simple harmonic motion, the acceleration is proportional to
In a simple harmonic motion
A small block oscillates back and forth on a smooth concave surface of radius R in Figure. Find the time period of small oscillation.

A simple pendulum fixed in a car has a time period of 4 seconds when the car is moving uniformly on a horizontal road. When the accelerator is pressed, the time period changes to 3.99 seconds. Making an approximate analysis, find the acceleration of the car.
Three simple harmonic motions of equal amplitude A and equal time periods in the same direction combine. The phase of the second motion is 60° ahead of the first and the phase of the third motion is 60° ahead of the second. Find the amplitude of the resultant motion.
A particle is subjected to two simple harmonic motions, one along the X-axis and the other on a line making an angle of 45° with the X-axis. The two motions are given by x = x0 sin ωt and s = s0 sin ωt. Find the amplitude of the resultant motion.
What is meant by simple harmonic oscillation? Give examples and explain why every simple harmonic motion is a periodic motion whereas the converse need not be true.
Describe Simple Harmonic Motion as a projection of uniform circular motion.
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
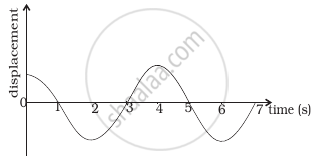
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
