Advertisements
Advertisements
प्रश्न
The angle made by the string of a simple pendulum with the vertical depends on time as \[\theta = \frac{\pi}{90} \sin \left[ \left( \pi s^{- 1} \right)t \right]\] .Find the length of the pendulum if g = π2 m2.
उत्तर
It is given that:
Angle made by the simple pendulum with the vertical, \[ \theta = \left( \frac{\pi}{90} \right)\sin \left[ \pi\left( s^{- 1} \right)t \right]\] On comparing the above equation with the equation of S . H . M . , we get:
\[\omega = \pi s^{- 1} \]
\[ \Rightarrow \frac{2\pi}{T} = \pi\]
\[ \therefore T = 2 s\]
\[\text { Time period is given by the relation, }\]
\[T = 2\pi\sqrt{\left( \frac{l}{g} \right)}\]
\[ \Rightarrow 2 = 2\pi\sqrt{\left( \frac{l}{\pi^2} \right)}\]
\[ \Rightarrow 1 = \pi\frac{1}{\pi}\sqrt{\left( l \right)}\]
\[ \Rightarrow l = 1 m\]
\[\text { Hence, length of the pendulum is 1 m .}\]
APPEARS IN
संबंधित प्रश्न
Which of the following relationships between the acceleration a and the displacement x of a particle involve simple harmonic motion?
(a) a = 0.7x
(b) a = –200x2
(c) a = –10x
(d) a = 100x3
Assuming the expression for displacement of a particle starting from extreme position, explain graphically the variation of velocity and acceleration w.r.t. time.
State the differential equation of linear simple harmonic motion.
A particle executing simple harmonic motion comes to rest at the extreme positions. Is the resultant force on the particle zero at these positions according to Newton's first law?
The energy of system in simple harmonic motion is given by \[E = \frac{1}{2}m \omega^2 A^2 .\] Which of the following two statements is more appropriate?
(A) The energy is increased because the amplitude is increased.
(B) The amplitude is increased because the energy is increased.
The distance moved by a particle in simple harmonic motion in one time period is
The motion of a particle is given by x = A sin ωt + B cos ωt. The motion of the particle is
The displacement of a particle is given by \[\overrightarrow{r} = A\left( \overrightarrow{i} \cos\omega t + \overrightarrow{j} \sin\omega t \right) .\] The motion of the particle is
For a particle executing simple harmonic motion, the acceleration is proportional to
In a simple harmonic motion
A pendulum clock giving correct time at a place where g = 9.800 m/s2 is taken to another place where it loses 24 seconds during 24 hours. Find the value of g at this new place.
A spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
A hollow sphere of radius 2 cm is attached to an 18 cm long thread to make a pendulum. Find the time period of oscillation of this pendulum. How does it differ from the time period calculated using the formula for a simple pendulum?
Three simple harmonic motions of equal amplitude A and equal time periods in the same direction combine. The phase of the second motion is 60° ahead of the first and the phase of the third motion is 60° ahead of the second. Find the amplitude of the resultant motion.
In a simple harmonic oscillation, the acceleration against displacement for one complete oscillation will be __________.
Write short notes on two springs connected in parallel.
The velocities of a particle in SHM at positions x1 and x2 are v1 and v2 respectively, its time period will be ______.
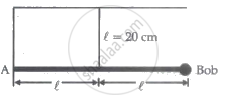
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20 cm, fixed at its midpoint. The bob is displaced slightly, perpendicular to the plane of the rod and string. The period of small oscillations of the system in the form `(pix)/10` is ______ sec. and the value of x is ______.
(g = 10 m/s2)