Advertisements
Advertisements
प्रश्न
Find the time period of small oscillations of the following systems. (a) A metre stick suspended through the 20 cm mark. (b) A ring of mass m and radius r suspended through a point on its periphery. (c) A uniform square plate of edge a suspended through a corner. (d) A uniform disc of mass m and radius r suspended through a point r/2 away from the centre.
उत्तर
(a) Moment Of inertia \[\left( I \right)\] about the point X is given by ,
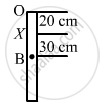
I = IC.G + mh2
\[= \frac{m l^2}{12} + m h^2 \]
\[ = \frac{m l^2}{12} + m \left( 0 . 3 \right)^2 \]
\[ = m\left( \frac{1}{12} + 0 . 09 \right)\]
\[ = m\left( \frac{1 + 1 . 08}{12} \right)\]
\[ = m\left( \frac{2 . 08}{12} \right)\]
The time Period \[\left( T \right)\] is given by,
\[T = 2\pi\sqrt{\frac{I}{mgl}}\] \[\text { where } I = \text{ the moment of inertia, and } \] \[ l= \text{ distance between the centre of gravity and the point of suspension . }\] \[\text {On substituting the respective values in the above formula, we get: }\] \[T = 2\pi\sqrt{\frac{2 . 08 m}{m \times 12 \times 9 . 8 \times 0 . 3}}\]
\[ = 1 . 52 s\]
(b) Moment Of inertia \[\left( I \right)\] about A is given as,
I = IC.G. + mr2 = mr2 + mr2 = 2mr2

The time period (T) will be,
\[T = 2\pi\sqrt{\frac{I}{mgl}}\]
\[\text { On substituting the respective values in the above equation, we have: }\]
\[T = 2\pi\sqrt{\frac{2m r^2}{mgr}}\]
\[ = 2\pi\sqrt{\frac{2r}{g}}\]
(c) Let I be the moment of inertia of a uniform square plate suspended through a corner.
\[I = m\left( \frac{a^2 + a^2}{3} \right) = \frac{2m}{3} a^2\]
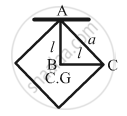
In the
\[\bigtriangleup\] ABC , l2 + l2 = a2
\[\therefore l = \frac{a}{\sqrt{2}}\]
\[ \Rightarrow T = 2\pi\sqrt{\frac{I}{mgl}}\]
\[ = 2\pi\sqrt{\frac{2m a^2}{3mgl}}\]
\[ = 2\pi\sqrt{\frac{2 a^2}{3ga\sqrt{2}}}\]
\[ = 2\pi\sqrt{\frac{\sqrt{8}a}{3g}}\]
(d)
\[\text { We know }\]
\[ h = \frac{r}{2}\]
\[\text { Distance between the C . G . and suspension point }, l = \frac{r}{2}\]
Moment of inertia about A will be:
l = IC.G. + mh2
\[= \frac{m r^2}{2} + m \left( \frac{r}{2} \right)^2 \]
\[ = m r^2 \left( \frac{1}{2} + \frac{1}{4} \right) = \frac{3}{4}m r^2\]
Time period (T) will be,
\[T = 2\pi\sqrt{\frac{I}{mgl}}\]
\[ = 2\pi\sqrt{\frac{3m r^2}{4mgl}} = 2\pi\sqrt{\frac{3r}{2g}}\]
APPEARS IN
संबंधित प्रश्न
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
General vibrations of a polyatomic molecule about its equilibrium position.
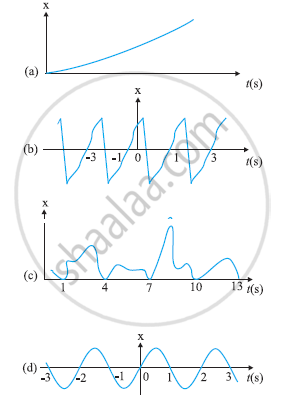
Figure depicts four x-t plots for linear motion of a particle. Which of the plots represent periodic motion? What is the period of motion (in case of periodic motion)?
The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 m. If the piston moves with simple harmonic motion with an angular frequency of 200 rad/min, what is its maximum speed?
A particle executes simple harmonic motion under the restoring force provided by a spring. The time period is T. If the spring is divided in two equal parts and one part is used to continue the simple harmonic motion, the time period will
A particle is fastened at the end of a string and is whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
The string the spring and the pulley shown in figure are light. Find the time period of the mass m.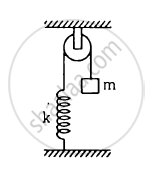
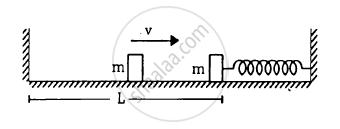
The left block in figure moves at a speed v towards the right block placed in equilibrium. All collisions to take place are elastic and the surfaces are frictionless. Show that the motions of the two blocks are periodic. Find the time period of these periodic motions. Neglect the widths of the blocks.
A body of mass 1 kg is mafe to oscillate on a spring of force constant 16 N/m. Calculate (a) Angular frequency, (b) Frequency of vibrations.
The period of oscillation of a body of mass m1 suspended from a light spring is T. When a body of mass m2 is tied to the first body and the system is made to oscillate, the period is 2T. Compare the masses m1 and m2
A 20 cm wide thin circular disc of mass 200 g is suspended to rigid support from a thin metallic string. By holding the rim of the disc, the string is twisted through 60° and released. It now performs angular oscillations of period 1 second. Calculate the maximum restoring torque generated in the string under undamped conditions. (π3 ≈ 31)
Which of the following example represent periodic motion?
A freely suspended bar magnet displaced from its N-S direction and released.
Which of the following example represent periodic motion?
A hydrogen molecule rotating about its center of mass.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
A motion of an oscillating mercury column in a U-tube.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
The motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lowermost point.
When two displacements represented by y1 = a sin(ωt) and y2 = b cos(ωt) are superimposed the motion is ______.
What are the two basic characteristics of a simple harmonic motion?
Show that the motion of a particle represented by y = sin ωt – cos ωt is simple harmonic with a period of 2π/ω.
The time period of a simple pendulum is T inside a lift when the lift is stationary. If the lift moves upwards with an acceleration `g/2`, the time period of the pendulum will be ______.
