Advertisements
Advertisements
प्रश्न
A spring stores 5 J of energy when stretched by 25 cm. It is kept vertical with the lower end fixed. A block fastened to its other end is made to undergo small oscillations. If the block makes 5 oscillations each second what is the mass of the block?
उत्तर
It is given that:
Energy stored in the spring, E = 5 J
Frequency of the mass-spring system, f = 5
Extension in the length of the spring, x = 25 cm = 0.25 m
\[\text { Time period }, T = \frac{1}{5} s\]
\[\text { Potential energy }\left( U \right)\text { is given by, } \]
\[U = \frac{1}{2}k x^2 \]
\[ \Rightarrow \frac{1}{2}k x^2 = 5\]
\[ \Rightarrow \frac{1}{2}k \left( 0 . 25 \right)^2 = 5\]
\[ \Rightarrow k = 160 N/m\]
\[\text { Time period of spring mass system is given by, }\]
\[ T = 2\pi\sqrt{\left( \frac{m}{k} \right)}\] \[ \text {where m is the mass of the body hanged, and }\] \[\text { k is the spring constant . }\]\[\text { On substituting the respective values in the above expression, we get: }\]
\[ \frac{1}{5} = 2\pi\sqrt{\left( \frac{m}{160} \right)}\]
\[ \Rightarrow m = 0 . 16 kg\]
APPEARS IN
संबंधित प्रश्न
A copper metal cube has each side of length 1 m. The bottom edge of the cube is fixed and tangential force 4.2x108 N is applied to a top surface. Calculate the lateral displacement of the top surface if modulus of rigidity of copper is 14x1010 N/m2.
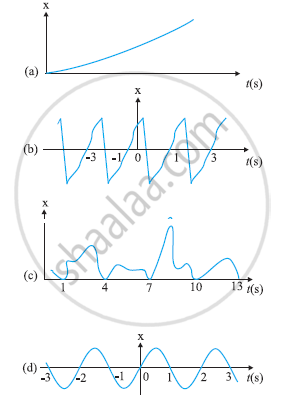
Figure depicts four x-t plots for linear motion of a particle. Which of the plots represent periodic motion? What is the period of motion (in case of periodic motion)?
The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 m. If the piston moves with simple harmonic motion with an angular frequency of 200 rad/min, what is its maximum speed?
A person goes to bed at sharp 10.00 pm every day. Is it an example of periodic motion? If yes, what is the time period? If no, why?
A particle is fastened at the end of a string and is whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
Consider a simple harmonic motion of time period T. Calculate the time taken for the displacement to change value from half the amplitude to the amplitude.
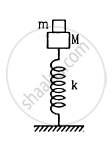
A small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscillates vertically. (a) Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. (b) Find the normal force on the smaller block at this position. When is this force smallest in magnitude? (c) What can be the maximum amplitude with which the two blocks may oscillate together?
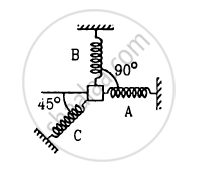
A particle of mass m is attatched to three springs A, B and C of equal force constants kas shown in figure . If the particle is pushed slightly against the spring C and released, find the time period of oscillation.
The string the spring and the pulley shown in figure are light. Find the time period of the mass m.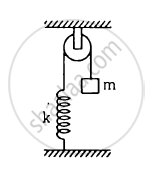
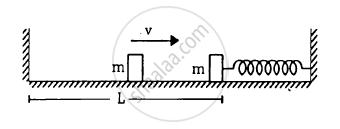
The left block in figure moves at a speed v towards the right block placed in equilibrium. All collisions to take place are elastic and the surfaces are frictionless. Show that the motions of the two blocks are periodic. Find the time period of these periodic motions. Neglect the widths of the blocks.
A uniform plate of mass M stays horizontally and symmetrically on two wheels rotating in opposite direction in Figure . The separation between the wheels is L. The friction coefficient between each wheel and the plate is μ. Find the time period of oscillation of the plate if it is slightly displaced along its length and released.

A 20 cm wide thin circular disc of mass 200 g is suspended to rigid support from a thin metallic string. By holding the rim of the disc, the string is twisted through 60° and released. It now performs angular oscillations of period 1 second. Calculate the maximum restoring torque generated in the string under undamped conditions. (π3 ≈ 31)
The maximum speed of a particle executing S.H.M. is 10 m/s and maximum acceleration is 31.4 m/s2. Its periodic time is ______
A simple pendulum is inside a spacecraft. What will be its periodic time?
Which of the following example represent periodic motion?
A hydrogen molecule rotating about its center of mass.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
The motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lowermost point.
Show that the motion of a particle represented by y = sin ωt – cos ωt is simple harmonic with a period of 2π/ω.
A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0 s–1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons weight against time.
- Will there be any change in weight of the body, during the oscillation?
- If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?
When a particle executes Simple Harmonic Motion, the nature of the graph of velocity as a function of displacement will be ______.
