Advertisements
Advertisements
Question
A spring stores 5 J of energy when stretched by 25 cm. It is kept vertical with the lower end fixed. A block fastened to its other end is made to undergo small oscillations. If the block makes 5 oscillations each second what is the mass of the block?
Solution
It is given that:
Energy stored in the spring, E = 5 J
Frequency of the mass-spring system, f = 5
Extension in the length of the spring, x = 25 cm = 0.25 m
\[\text { Time period }, T = \frac{1}{5} s\]
\[\text { Potential energy }\left( U \right)\text { is given by, } \]
\[U = \frac{1}{2}k x^2 \]
\[ \Rightarrow \frac{1}{2}k x^2 = 5\]
\[ \Rightarrow \frac{1}{2}k \left( 0 . 25 \right)^2 = 5\]
\[ \Rightarrow k = 160 N/m\]
\[\text { Time period of spring mass system is given by, }\]
\[ T = 2\pi\sqrt{\left( \frac{m}{k} \right)}\] \[ \text {where m is the mass of the body hanged, and }\] \[\text { k is the spring constant . }\]\[\text { On substituting the respective values in the above expression, we get: }\]
\[ \frac{1}{5} = 2\pi\sqrt{\left( \frac{m}{160} \right)}\]
\[ \Rightarrow m = 0 . 16 kg\]
APPEARS IN
RELATED QUESTIONS
A copper metal cube has each side of length 1 m. The bottom edge of the cube is fixed and tangential force 4.2x108 N is applied to a top surface. Calculate the lateral displacement of the top surface if modulus of rigidity of copper is 14x1010 N/m2.
Which of the following example represent periodic motion?
An arrow released from a bow.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
General vibrations of a polyatomic molecule about its equilibrium position.
The length of the second’s pendulum in a clock is increased to 4 times its initial length. Calculate the number of oscillations completed by the new pendulum in one minute.
A particle executes simple harmonic motion with a frequency v. The frequency with which the kinetic energy oscillates is
The position, velocity and acceleration of a particle executing simple harmonic motion are found to have magnitude 2 cm, 1 m s−1 and 10 m s−2 at a certain instant. Find the amplitude and the time period of the motion.
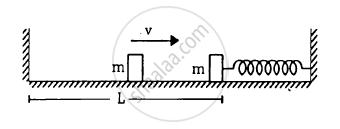
The left block in figure moves at a speed v towards the right block placed in equilibrium. All collisions to take place are elastic and the surfaces are frictionless. Show that the motions of the two blocks are periodic. Find the time period of these periodic motions. Neglect the widths of the blocks.
Find the time period of small oscillations of the following systems. (a) A metre stick suspended through the 20 cm mark. (b) A ring of mass m and radius r suspended through a point on its periphery. (c) A uniform square plate of edge a suspended through a corner. (d) A uniform disc of mass m and radius r suspended through a point r/2 away from the centre.
A uniform disc of radius r is to be suspended through a small hole made in the disc. Find the minimum possible time period of the disc for small oscillations. What should be the distance of the hole from the centre for it to have minimum time period?
The period of oscillation of a body of mass m1 suspended from a light spring is T. When a body of mass m2 is tied to the first body and the system is made to oscillate, the period is 2T. Compare the masses m1 and m2
Which of the following example represent periodic motion?
A hydrogen molecule rotating about its center of mass.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
The motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lowermost point.
When two displacements represented by y1 = a sin(ωt) and y2 = b cos(ωt) are superimposed the motion is ______.
What are the two basic characteristics of a simple harmonic motion?
A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0 s–1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons weight against time.
- Will there be any change in weight of the body, during the oscillation?
- If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?
The time period of a simple pendulum is T inside a lift when the lift is stationary. If the lift moves upwards with an acceleration `g/2`, the time period of the pendulum will be ______.
When a particle executes Simple Harmonic Motion, the nature of the graph of velocity as a function of displacement will be ______.
