Advertisements
Advertisements
Question
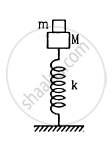
A small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscillates vertically. (a) Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. (b) Find the normal force on the smaller block at this position. When is this force smallest in magnitude? (c) What can be the maximum amplitude with which the two blocks may oscillate together?
Solution
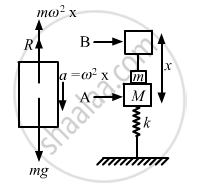
(a) Consider the free body diagram.
Weight of the body, W = mg
Force, F = ma = mω2x
x is the small displacement of mass m.
As normal reaction R is acting vertically in the upward direction, we can write:
R + mω2x − mg = 0 ....(1)
Resultant force = mω2x = mg − R
\[\Rightarrow m \omega^2 x = m\left( \frac{k}{M + m} \right)x\]
\[ = \frac{mkx}{M + m}\]
\[\text { Here }, \]
\[\omega = \sqrt{\left\{ \frac{k}{M + m} \right\}}\]
(b) R = mg − mω2x
\[= mg - m\frac{k}{M + N}x\]
\[ = mg - \frac{mkx}{M + N}\]
It can be seen from the above equations that, for R to be smallest, the value of mω2xshould be maximum which is only possible when the particle is at the highest point.
(c) R = mg − mω2x
As the two blocks oscillate together R becomes greater than zero.
When limiting condition follows,
i.e. R = 0
mg = mω2x
\[x = \frac{mg}{m \omega^2} = \frac{mg \cdot \left( M + m \right)}{mk}\]
Required maximum amplitude
\[= \frac{g\left( M + m \right)}{k}\]
APPEARS IN
RELATED QUESTIONS
The periodic time of a linear harmonic oscillator is 2π second, with maximum displacement of 1 cm. If the particle starts from extreme position, find the displacement of the particle after π/3 seconds.
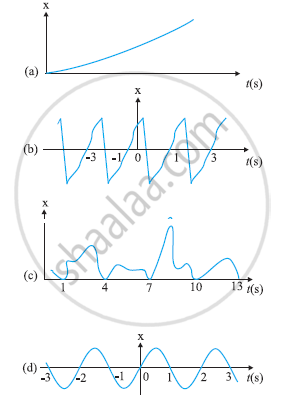
Figure depicts four x-t plots for linear motion of a particle. Which of the plots represent periodic motion? What is the period of motion (in case of periodic motion)?
The total mechanical energy of a spring-mass system in simple harmonic motion is \[E = \frac{1}{2}m \omega^2 A^2 .\] Suppose the oscillating particle is replaced by another particle of double the mass while the amplitude A remains the same. The new mechanical energy will
A particle moves in a circular path with a uniform speed. Its motion is
The position, velocity and acceleration of a particle executing simple harmonic motion are found to have magnitude 2 cm, 1 m s−1 and 10 m s−2 at a certain instant. Find the amplitude and the time period of the motion.
A uniform plate of mass M stays horizontally and symmetrically on two wheels rotating in opposite direction in Figure . The separation between the wheels is L. The friction coefficient between each wheel and the plate is μ. Find the time period of oscillation of the plate if it is slightly displaced along its length and released.

The ear-ring of a lady shown in figure has a 3 cm long light suspension wire. (a) Find the time period of small oscillations if the lady is standing on the ground. (b) The lady now sits in a merry-go-round moving at 4 m/s1 in a circle of radius 2 m. Find the time period of small oscillations of the ear-ring.

A 20 cm wide thin circular disc of mass 200 g is suspended to rigid support from a thin metallic string. By holding the rim of the disc, the string is twisted through 60° and released. It now performs angular oscillations of period 1 second. Calculate the maximum restoring torque generated in the string under undamped conditions. (π3 ≈ 31)
The maximum speed of a particle executing S.H.M. is 10 m/s and maximum acceleration is 31.4 m/s2. Its periodic time is ______
Which of the following example represent periodic motion?
A swimmer completing one (return) trip from one bank of a river to the other and back.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
A motion of an oscillating mercury column in a U-tube.
A simple pendulum of frequency n falls freely under gravity from a certain height from the ground level. Its frequency of oscillation.
The equation of motion of a particle is x = a cos (αt)2. The motion is ______.
The time period of a simple pendulum is T inside a lift when the lift is stationary. If the lift moves upwards with an acceleration `g/2`, the time period of the pendulum will be ______.
When a particle executes Simple Harmonic Motion, the nature of the graph of velocity as a function of displacement will be ______.
A particle performs simple harmonic motion with a period of 2 seconds. The time taken by the particle to cover a displacement equal to half of its amplitude from the mean position is `1/a` s. The value of 'a' to the nearest integer is ______.
