Advertisements
Advertisements
प्रश्न
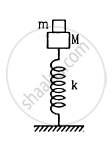
A small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscillates vertically. (a) Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. (b) Find the normal force on the smaller block at this position. When is this force smallest in magnitude? (c) What can be the maximum amplitude with which the two blocks may oscillate together?
उत्तर
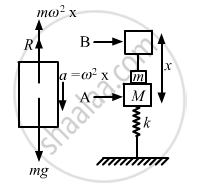
(a) Consider the free body diagram.
Weight of the body, W = mg
Force, F = ma = mω2x
x is the small displacement of mass m.
As normal reaction R is acting vertically in the upward direction, we can write:
R + mω2x − mg = 0 ....(1)
Resultant force = mω2x = mg − R
\[\Rightarrow m \omega^2 x = m\left( \frac{k}{M + m} \right)x\]
\[ = \frac{mkx}{M + m}\]
\[\text { Here }, \]
\[\omega = \sqrt{\left\{ \frac{k}{M + m} \right\}}\]
(b) R = mg − mω2x
\[= mg - m\frac{k}{M + N}x\]
\[ = mg - \frac{mkx}{M + N}\]
It can be seen from the above equations that, for R to be smallest, the value of mω2xshould be maximum which is only possible when the particle is at the highest point.
(c) R = mg − mω2x
As the two blocks oscillate together R becomes greater than zero.
When limiting condition follows,
i.e. R = 0
mg = mω2x
\[x = \frac{mg}{m \omega^2} = \frac{mg \cdot \left( M + m \right)}{mk}\]
Required maximum amplitude
\[= \frac{g\left( M + m \right)}{k}\]
APPEARS IN
संबंधित प्रश्न
A seconds pendulum is suspended in an elevator moving with constant speed in downward direction. The periodic time (T) of that pendulum is _______.
Which of the following example represent periodic motion?
An arrow released from a bow.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
General vibrations of a polyatomic molecule about its equilibrium position.
The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 m. If the piston moves with simple harmonic motion with an angular frequency of 200 rad/min, what is its maximum speed?
The length of the second’s pendulum in a clock is increased to 4 times its initial length. Calculate the number of oscillations completed by the new pendulum in one minute.
Two bodies A and B of equal mass are suspended from two separate massless springs of spring constant k1 and k2 respectively. If the bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of A to that of B is
A spring stores 5 J of energy when stretched by 25 cm. It is kept vertical with the lower end fixed. A block fastened to its other end is made to undergo small oscillations. If the block makes 5 oscillations each second what is the mass of the block?
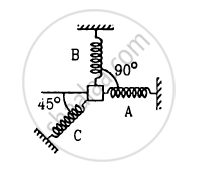
A particle of mass m is attatched to three springs A, B and C of equal force constants kas shown in figure . If the particle is pushed slightly against the spring C and released, find the time period of oscillation.
The ear-ring of a lady shown in figure has a 3 cm long light suspension wire. (a) Find the time period of small oscillations if the lady is standing on the ground. (b) The lady now sits in a merry-go-round moving at 4 m/s1 in a circle of radius 2 m. Find the time period of small oscillations of the ear-ring.

Find the time period of small oscillations of the following systems. (a) A metre stick suspended through the 20 cm mark. (b) A ring of mass m and radius r suspended through a point on its periphery. (c) A uniform square plate of edge a suspended through a corner. (d) A uniform disc of mass m and radius r suspended through a point r/2 away from the centre.
A 20 cm wide thin circular disc of mass 200 g is suspended to rigid support from a thin metallic string. By holding the rim of the disc, the string is twisted through 60° and released. It now performs angular oscillations of period 1 second. Calculate the maximum restoring torque generated in the string under undamped conditions. (π3 ≈ 31)
Which of the following example represent periodic motion?
A freely suspended bar magnet displaced from its N-S direction and released.
Which of the following example represent periodic motion?
A hydrogen molecule rotating about its center of mass.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
The rotation of the earth about its axis.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
A motion of an oscillating mercury column in a U-tube.
When two displacements represented by y1 = a sin(ωt) and y2 = b cos(ωt) are superimposed the motion is ______.
Show that the motion of a particle represented by y = sin ωt – cos ωt is simple harmonic with a period of 2π/ω.
