Advertisements
Advertisements
Question
The left block in figure moves at a speed v towards the right block placed in equilibrium. All collisions to take place are elastic and the surfaces are frictionless. Show that the motions of the two blocks are periodic. Find the time period of these periodic motions. Neglect the widths of the blocks.
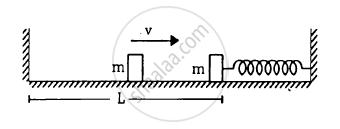
Solution
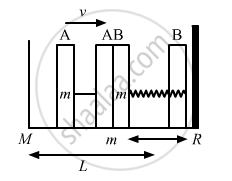
According to the question, the collision is elastic and the surface is frictionless, therefore, when the left block A moves with speed v and collides with the right block B, it transfers all the energy to the right block B.
The left block A moves a distance x against the spring; the right block returns to the original position and completes half of the oscillation.
Therefore, the period of right block B will be, \[T = \frac{2\pi\sqrt{\left( \frac{m}{k} \right)}}{2} = \pi\sqrt{\left( \frac{m}{k} \right)}\]
Right block B collides with left block A and comes to rest.
Let L be the distance moved by the block to return to its original position.
The time taken is given by,
\[\frac{L}{V} + \frac{L}{V} = 2\left( \frac{L}{V} \right)\]
Hence, time period of the periodic motion is,
APPEARS IN
RELATED QUESTIONS
Which of the following example represent periodic motion?
An arrow released from a bow.
The total mechanical energy of a spring-mass system in simple harmonic motion is \[E = \frac{1}{2}m \omega^2 A^2 .\] Suppose the oscillating particle is replaced by another particle of double the mass while the amplitude A remains the same. The new mechanical energy will
A particle moves in a circular path with a uniform speed. Its motion is
Consider a simple harmonic motion of time period T. Calculate the time taken for the displacement to change value from half the amplitude to the amplitude.
A spring stores 5 J of energy when stretched by 25 cm. It is kept vertical with the lower end fixed. A block fastened to its other end is made to undergo small oscillations. If the block makes 5 oscillations each second what is the mass of the block?
Find the number of oscillations performed per minute by a magnet is vibrating in the plane of a uniform field of 1.6 × 10-5 Wb/m2. The magnet has a moment of inertia 3 × 10-6 kg/m2 and magnetic moment 3 A m2.
The maximum speed of a particle executing S.H.M. is 10 m/s and maximum acceleration is 31.4 m/s2. Its periodic time is ______
A simple pendulum is inside a spacecraft. What will be its periodic time?
Which of the following example represent periodic motion?
A hydrogen molecule rotating about its center of mass.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
The rotation of the earth about its axis.
When two displacements represented by y1 = a sin(ωt) and y2 = b cos(ωt) are superimposed the motion is ______.
A simple pendulum of frequency n falls freely under gravity from a certain height from the ground level. Its frequency of oscillation.
What are the two basic characteristics of a simple harmonic motion?
A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0 s–1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons weight against time.
- Will there be any change in weight of the body, during the oscillation?
- If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?
A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0 s–1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons weight against time.
- Will there be any change in weight of the body, during the oscillation?
- If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?
The time period of a simple pendulum is T inside a lift when the lift is stationary. If the lift moves upwards with an acceleration `g/2`, the time period of the pendulum will be ______.
When a particle executes Simple Harmonic Motion, the nature of the graph of velocity as a function of displacement will be ______.
A particle performs simple harmonic motion with a period of 2 seconds. The time taken by the particle to cover a displacement equal to half of its amplitude from the mean position is `1/a` s. The value of 'a' to the nearest integer is ______.
