Advertisements
Advertisements
प्रश्न
The left block in figure moves at a speed v towards the right block placed in equilibrium. All collisions to take place are elastic and the surfaces are frictionless. Show that the motions of the two blocks are periodic. Find the time period of these periodic motions. Neglect the widths of the blocks.
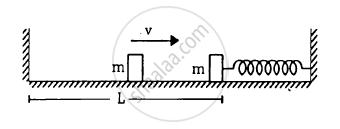
उत्तर
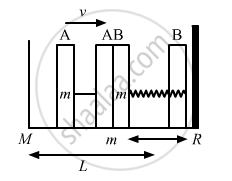
According to the question, the collision is elastic and the surface is frictionless, therefore, when the left block A moves with speed v and collides with the right block B, it transfers all the energy to the right block B.
The left block A moves a distance x against the spring; the right block returns to the original position and completes half of the oscillation.
Therefore, the period of right block B will be, \[T = \frac{2\pi\sqrt{\left( \frac{m}{k} \right)}}{2} = \pi\sqrt{\left( \frac{m}{k} \right)}\]
Right block B collides with left block A and comes to rest.
Let L be the distance moved by the block to return to its original position.
The time taken is given by,
\[\frac{L}{V} + \frac{L}{V} = 2\left( \frac{L}{V} \right)\]
Hence, time period of the periodic motion is,
APPEARS IN
संबंधित प्रश्न
The periodic time of a linear harmonic oscillator is 2π second, with maximum displacement of 1 cm. If the particle starts from extreme position, find the displacement of the particle after π/3 seconds.
Which of the following example represent periodic motion?
An arrow released from a bow.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
General vibrations of a polyatomic molecule about its equilibrium position.
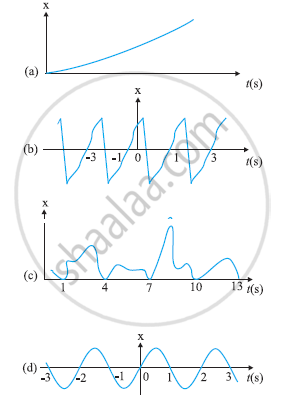
Figure depicts four x-t plots for linear motion of a particle. Which of the plots represent periodic motion? What is the period of motion (in case of periodic motion)?
Answer in brief:
Derive an expression for the period of motion of a simple pendulum. On which factors does it depend?
A particle executes simple harmonic motion with a frequency v. The frequency with which the kinetic energy oscillates is
A particle executes simple harmonic motion under the restoring force provided by a spring. The time period is T. If the spring is divided in two equal parts and one part is used to continue the simple harmonic motion, the time period will
A particle is fastened at the end of a string and is whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
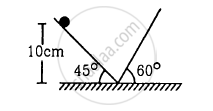
Find the time period of the motion of the particle shown in figure . Neglect the small effect of the bend near the bottom.
The ear-ring of a lady shown in figure has a 3 cm long light suspension wire. (a) Find the time period of small oscillations if the lady is standing on the ground. (b) The lady now sits in a merry-go-round moving at 4 m/s1 in a circle of radius 2 m. Find the time period of small oscillations of the ear-ring.

Which of the following example represent periodic motion?
A swimmer completing one (return) trip from one bank of a river to the other and back.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
The rotation of the earth about its axis.
When two displacements represented by y1 = a sin(ωt) and y2 = b cos(ωt) are superimposed the motion is ______.
A simple pendulum of frequency n falls freely under gravity from a certain height from the ground level. Its frequency of oscillation.
Show that the motion of a particle represented by y = sin ωt – cos ωt is simple harmonic with a period of 2π/ω.
When a particle executes Simple Harmonic Motion, the nature of the graph of velocity as a function of displacement will be ______.
A particle performs simple harmonic motion with a period of 2 seconds. The time taken by the particle to cover a displacement equal to half of its amplitude from the mean position is `1/a` s. The value of 'a' to the nearest integer is ______.
