Advertisements
Advertisements
प्रश्न
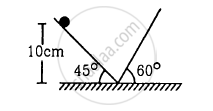
Find the time period of the motion of the particle shown in figure . Neglect the small effect of the bend near the bottom.
उत्तर
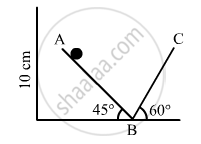
Let t1 and t2 be the time taken by the particle to travel distances AB and BC respectively.
Acceleration for part AB, a1 = g sin 45°
The distance travelled along AB is s1.
\[\therefore s_1 = \frac{0 . 1}{\sin 45^\circ} = 2 m\]
Let v be the velocity at point B, and
u be the initial velocity.
Using the third equation of motion, we have:
v2 − u2 = 2a1s1
\[\Rightarrow v^2 = 2 \times g \sin 45^\circ\times \frac{0 . 1}{\sin 45^\circ} = 2\]
\[ \Rightarrow v = \sqrt{2} m/s\]
\[As v = u + a_1 t_1 \]
\[ \therefore t_1 = \frac{v - u}{a_1}\]
\[ = \frac{\sqrt{2} - 0}{\frac{g}{\sqrt{2}}}\]
\[ = \frac{2}{g} = \frac{2}{10} = 0 . 2 \sec \ ( g = 10 {ms}^{- 2} )\]
For the distance BC,
Acceleration, a2 =\[-\]gsin 60°
\[\text { Initial velocity }, u = \sqrt{2} \]
\[ v = 0\]
\[ \therefore \text { time period }, t_2 = \frac{0 - \sqrt{2}}{- \frac{g}{\left( 3\sqrt{2} \right)}} = \frac{2\sqrt{2}}{\sqrt{3}g}\]
\[ = \frac{2 \times \left( 1 . 414 \right)}{\left( 1 . 732 \right) \times 10} = 0 . 163 s\]
Thus, the total time period, t = 2(t1 + t2) = 2 (0.2 + 0.163) = 0.73 s
APPEARS IN
संबंधित प्रश्न
The periodic time of a linear harmonic oscillator is 2π second, with maximum displacement of 1 cm. If the particle starts from extreme position, find the displacement of the particle after π/3 seconds.
A copper metal cube has each side of length 1 m. The bottom edge of the cube is fixed and tangential force 4.2x108 N is applied to a top surface. Calculate the lateral displacement of the top surface if modulus of rigidity of copper is 14x1010 N/m2.
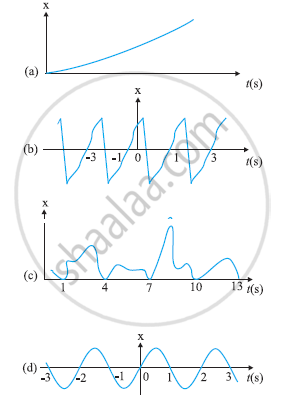
Figure depicts four x-t plots for linear motion of a particle. Which of the plots represent periodic motion? What is the period of motion (in case of periodic motion)?
Answer in brief:
Derive an expression for the period of motion of a simple pendulum. On which factors does it depend?
A particle executes simple harmonic motion with a frequency v. The frequency with which the kinetic energy oscillates is
A particle executes simple harmonic motion under the restoring force provided by a spring. The time period is T. If the spring is divided in two equal parts and one part is used to continue the simple harmonic motion, the time period will
A uniform plate of mass M stays horizontally and symmetrically on two wheels rotating in opposite direction in Figure . The separation between the wheels is L. The friction coefficient between each wheel and the plate is μ. Find the time period of oscillation of the plate if it is slightly displaced along its length and released.

A uniform disc of radius r is to be suspended through a small hole made in the disc. Find the minimum possible time period of the disc for small oscillations. What should be the distance of the hole from the centre for it to have minimum time period?
A body of mass 1 kg is mafe to oscillate on a spring of force constant 16 N/m. Calculate (a) Angular frequency, (b) Frequency of vibrations.
The period of oscillation of a body of mass m1 suspended from a light spring is T. When a body of mass m2 is tied to the first body and the system is made to oscillate, the period is 2T. Compare the masses m1 and m2
The maximum speed of a particle executing S.H.M. is 10 m/s and maximum acceleration is 31.4 m/s2. Its periodic time is ______
A simple pendulum is inside a spacecraft. What will be its periodic time?
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
The rotation of the earth about its axis.
The displacement time graph of a particle executing S.H.M. is shown in figure. Which of the following statement is/are true?
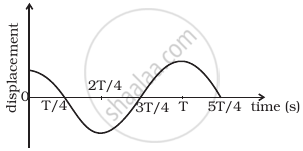
- The force is zero at `t = (T)/4`.
- The acceleration is maximum at `t = (4T)/4`.
- The velocity is maximum at `t = T/4`.
- The P.E. is equal to K.E. of oscillation at `t = T/2`.
Show that the motion of a particle represented by y = sin ωt – cos ωt is simple harmonic with a period of 2π/ω.
When a particle executes Simple Harmonic Motion, the nature of the graph of velocity as a function of displacement will be ______.
