Advertisements
Advertisements
प्रश्न
A copper metal cube has each side of length 1 m. The bottom edge of the cube is fixed and tangential force 4.2x108 N is applied to a top surface. Calculate the lateral displacement of the top surface if modulus of rigidity of copper is 14x1010 N/m2.
उत्तर
Given
η=14x1010 N/m
F=4.2x108 N
A=1x1=1m2
`eta=(Fh)/(Ax)`
`x=(Fh)/(Aeta)`
`=(4.2xx10^8xx1m)/(1xx14xx10^10)`
`=(4.2xx10^8)/(14xx10^10)`
=0.3x10-2m=3mm
APPEARS IN
संबंधित प्रश्न
A seconds pendulum is suspended in an elevator moving with constant speed in downward direction. The periodic time (T) of that pendulum is _______.
The periodic time of a linear harmonic oscillator is 2π second, with maximum displacement of 1 cm. If the particle starts from extreme position, find the displacement of the particle after π/3 seconds.
Which of the following example represent periodic motion?
An arrow released from a bow.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
General vibrations of a polyatomic molecule about its equilibrium position.
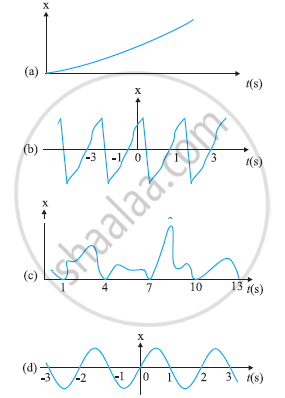
Figure depicts four x-t plots for linear motion of a particle. Which of the plots represent periodic motion? What is the period of motion (in case of periodic motion)?
The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 m. If the piston moves with simple harmonic motion with an angular frequency of 200 rad/min, what is its maximum speed?
The length of the second’s pendulum in a clock is increased to 4 times its initial length. Calculate the number of oscillations completed by the new pendulum in one minute.
A person goes to bed at sharp 10.00 pm every day. Is it an example of periodic motion? If yes, what is the time period? If no, why?
The total mechanical energy of a spring-mass system in simple harmonic motion is \[E = \frac{1}{2}m \omega^2 A^2 .\] Suppose the oscillating particle is replaced by another particle of double the mass while the amplitude A remains the same. The new mechanical energy will
A particle executes simple harmonic motion with a frequency v. The frequency with which the kinetic energy oscillates is
A particle executes simple harmonic motion under the restoring force provided by a spring. The time period is T. If the spring is divided in two equal parts and one part is used to continue the simple harmonic motion, the time period will
Two bodies A and B of equal mass are suspended from two separate massless springs of spring constant k1 and k2 respectively. If the bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of A to that of B is
A particle moves in a circular path with a uniform speed. Its motion is
The position, velocity and acceleration of a particle executing simple harmonic motion are found to have magnitude 2 cm, 1 m s−1 and 10 m s−2 at a certain instant. Find the amplitude and the time period of the motion.
Consider a simple harmonic motion of time period T. Calculate the time taken for the displacement to change value from half the amplitude to the amplitude.
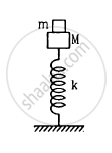
A small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscillates vertically. (a) Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. (b) Find the normal force on the smaller block at this position. When is this force smallest in magnitude? (c) What can be the maximum amplitude with which the two blocks may oscillate together?
The string the spring and the pulley shown in figure are light. Find the time period of the mass m.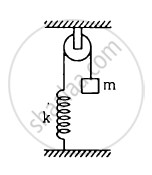
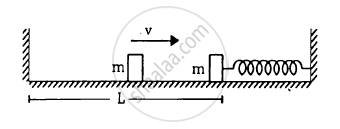
The left block in figure moves at a speed v towards the right block placed in equilibrium. All collisions to take place are elastic and the surfaces are frictionless. Show that the motions of the two blocks are periodic. Find the time period of these periodic motions. Neglect the widths of the blocks.
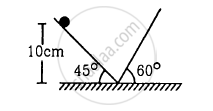
Find the time period of the motion of the particle shown in figure . Neglect the small effect of the bend near the bottom.
A uniform plate of mass M stays horizontally and symmetrically on two wheels rotating in opposite direction in Figure . The separation between the wheels is L. The friction coefficient between each wheel and the plate is μ. Find the time period of oscillation of the plate if it is slightly displaced along its length and released.

Find the time period of small oscillations of the following systems. (a) A metre stick suspended through the 20 cm mark. (b) A ring of mass m and radius r suspended through a point on its periphery. (c) A uniform square plate of edge a suspended through a corner. (d) A uniform disc of mass m and radius r suspended through a point r/2 away from the centre.
A uniform disc of radius r is to be suspended through a small hole made in the disc. Find the minimum possible time period of the disc for small oscillations. What should be the distance of the hole from the centre for it to have minimum time period?
The period of oscillation of a body of mass m1 suspended from a light spring is T. When a body of mass m2 is tied to the first body and the system is made to oscillate, the period is 2T. Compare the masses m1 and m2
Find the number of oscillations performed per minute by a magnet is vibrating in the plane of a uniform field of 1.6 × 10-5 Wb/m2. The magnet has a moment of inertia 3 × 10-6 kg/m2 and magnetic moment 3 A m2.
Which of the following example represent periodic motion?
A swimmer completing one (return) trip from one bank of a river to the other and back.
Which of the following example represent periodic motion?
A freely suspended bar magnet displaced from its N-S direction and released.
Which of the following example represent periodic motion?
A hydrogen molecule rotating about its center of mass.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
The rotation of the earth about its axis.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
A motion of an oscillating mercury column in a U-tube.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
The motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lowermost point.
When two displacements represented by y1 = a sin(ωt) and y2 = b cos(ωt) are superimposed the motion is ______.
The displacement time graph of a particle executing S.H.M. is shown in figure. Which of the following statement is/are true?
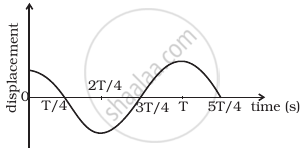
- The force is zero at `t = (T)/4`.
- The acceleration is maximum at `t = (4T)/4`.
- The velocity is maximum at `t = T/4`.
- The P.E. is equal to K.E. of oscillation at `t = T/2`.
What are the two basic characteristics of a simple harmonic motion?
A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0 s–1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons weight against time.
- Will there be any change in weight of the body, during the oscillation?
- If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?
A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0 s–1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons weight against time.
- Will there be any change in weight of the body, during the oscillation?
- If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?
