Advertisements
Advertisements
प्रश्न
A uniform plate of mass M stays horizontally and symmetrically on two wheels rotating in opposite direction in Figure . The separation between the wheels is L. The friction coefficient between each wheel and the plate is μ. Find the time period of oscillation of the plate if it is slightly displaced along its length and released.

उत्तर
Let x be the displacement of the uniform plate towards left.
Therefore, the centre of gravity will also be displaced through displacement x.
At the displaced position,
R1 + R2 = mg
Taking moment about g, we get:
\[R_1 \left( \frac{L}{2} - x \right) = R_2 \left( \frac{L}{2} + x \right) = \left( Mg - R_1 \right) \left( \frac{L}{2} + x \right) . . . . \left( 1 \right)\]
\[ \therefore R_1 \left( \frac{L}{2} - x \right) = \left( Mg - R_1 \right) \left( \frac{L}{2} + x \right)\]
\[ \Rightarrow R_1 \frac{L}{2} - R_1 x = Mg\frac{L}{2} - R_1 x + Mgx - R_1 \frac{L}{2}\]
\[ \Rightarrow R_1 \frac{L}{2} + R_1 \frac{L}{2} = Mg\left( x + \frac{L}{2} \right)\]
\[ \Rightarrow R_1 \left( \frac{L}{2} + \frac{L}{2} \right) = Mg\left( \frac{2x + L}{2} \right)\]
\[ \Rightarrow R_1 L = Mg\left( 2x + L \right)\]
\[ \Rightarrow R_1 = Mg\frac{\left( L + 2x \right)}{2L}\]
\[\text { Now }, \]
\[ F_1 = \mu R_1 = \mu Mg\frac{\left( L + 2x \right)}{2L}\]
\[\text { Similarly }, \]
\[ F_2 = \mu R_2 = \mu Mg\frac{\left( L - 2x \right)}{2L}\]
\[\text { As } F_1 > F_2 , \text { we can write: }\]
\[ F_1 - F_2 = Ma = \left( 2\mu\frac{Mg}{L} \right)x\]
\[ \frac{a}{x} = 2\mu\frac{g}{L} = \omega^2 \]
\[ \Rightarrow \omega = \sqrt{\frac{2\mu g}{L}}\]
\[\text { Time period }\left( T \right)\text{ is given by }, \]
\[T = 2\pi\sqrt{\frac{L}{2\mu g}}\]
APPEARS IN
संबंधित प्रश्न
The length of the second’s pendulum in a clock is increased to 4 times its initial length. Calculate the number of oscillations completed by the new pendulum in one minute.
The total mechanical energy of a spring-mass system in simple harmonic motion is \[E = \frac{1}{2}m \omega^2 A^2 .\] Suppose the oscillating particle is replaced by another particle of double the mass while the amplitude A remains the same. The new mechanical energy will
A particle executes simple harmonic motion under the restoring force provided by a spring. The time period is T. If the spring is divided in two equal parts and one part is used to continue the simple harmonic motion, the time period will
A particle is fastened at the end of a string and is whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
The position, velocity and acceleration of a particle executing simple harmonic motion are found to have magnitude 2 cm, 1 m s−1 and 10 m s−2 at a certain instant. Find the amplitude and the time period of the motion.
Consider a simple harmonic motion of time period T. Calculate the time taken for the displacement to change value from half the amplitude to the amplitude.
A spring stores 5 J of energy when stretched by 25 cm. It is kept vertical with the lower end fixed. A block fastened to its other end is made to undergo small oscillations. If the block makes 5 oscillations each second what is the mass of the block?
The string the spring and the pulley shown in figure are light. Find the time period of the mass m.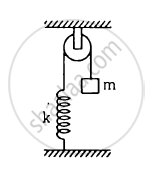
The ear-ring of a lady shown in figure has a 3 cm long light suspension wire. (a) Find the time period of small oscillations if the lady is standing on the ground. (b) The lady now sits in a merry-go-round moving at 4 m/s1 in a circle of radius 2 m. Find the time period of small oscillations of the ear-ring.

Find the time period of small oscillations of the following systems. (a) A metre stick suspended through the 20 cm mark. (b) A ring of mass m and radius r suspended through a point on its periphery. (c) A uniform square plate of edge a suspended through a corner. (d) A uniform disc of mass m and radius r suspended through a point r/2 away from the centre.
The maximum speed of a particle executing S.H.M. is 10 m/s and maximum acceleration is 31.4 m/s2. Its periodic time is ______
Which of the following example represent periodic motion?
A swimmer completing one (return) trip from one bank of a river to the other and back.
Which of the following example represent periodic motion?
A hydrogen molecule rotating about its center of mass.
The equation of motion of a particle is x = a cos (αt)2. The motion is ______.
What are the two basic characteristics of a simple harmonic motion?
Show that the motion of a particle represented by y = sin ωt – cos ωt is simple harmonic with a period of 2π/ω.
A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0 s–1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons weight against time.
- Will there be any change in weight of the body, during the oscillation?
- If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?
A particle performs simple harmonic motion with a period of 2 seconds. The time taken by the particle to cover a displacement equal to half of its amplitude from the mean position is `1/a` s. The value of 'a' to the nearest integer is ______.
