Advertisements
Advertisements
प्रश्न
The equation of motion of a particle is x = a cos (αt)2. The motion is ______.
विकल्प
periodic but not oscillatory.
periodic and oscillatory.
oscillatory but not periodic.
neither periodic nor oscillatory.
उत्तर
The equation of motion of a particle is x = a cos (αt)2. The motion is oscillatory but not periodic.
Explanation:
As the given equation is x = a cos (αt)2 is a cosine function. Hence, it is an oscillatory motion.
Now, putting t + T in place of t
x(t + T) = a cos [α(t + T)]2 .....[∵ x(t) = a cos(αt)2]
= a cos[αt2 + αT2 + 2α t T] ≠ x (t)
Where T is supposed as a period of the function ω(t).
Hence, it is not periodic.
APPEARS IN
संबंधित प्रश्न
A copper metal cube has each side of length 1 m. The bottom edge of the cube is fixed and tangential force 4.2x108 N is applied to a top surface. Calculate the lateral displacement of the top surface if modulus of rigidity of copper is 14x1010 N/m2.
Answer in brief:
Derive an expression for the period of motion of a simple pendulum. On which factors does it depend?
Consider a simple harmonic motion of time period T. Calculate the time taken for the displacement to change value from half the amplitude to the amplitude.
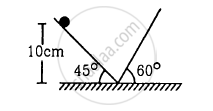
Find the time period of the motion of the particle shown in figure . Neglect the small effect of the bend near the bottom.
A uniform plate of mass M stays horizontally and symmetrically on two wheels rotating in opposite direction in Figure . The separation between the wheels is L. The friction coefficient between each wheel and the plate is μ. Find the time period of oscillation of the plate if it is slightly displaced along its length and released.

A body of mass 1 kg is mafe to oscillate on a spring of force constant 16 N/m. Calculate (a) Angular frequency, (b) Frequency of vibrations.
The maximum speed of a particle executing S.H.M. is 10 m/s and maximum acceleration is 31.4 m/s2. Its periodic time is ______
Which of the following example represent periodic motion?
A hydrogen molecule rotating about its center of mass.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
The rotation of the earth about its axis.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
The motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lowermost point.
