Advertisements
Advertisements
Question
A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0 s–1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons weight against time.
- Will there be any change in weight of the body, during the oscillation?
- If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?
Advertisements
Solution
In this case, acceleration is variable. In accelerated motion, the weight of body depends on the magnitude and direction of acceleration for upward or downward motion.
a. Hence, the weight of the body changes during oscillations
b. Considering the situation in two extreme positions. as their acceleration is maximum in magnitude.
We have, mg – N = ma
∵ At the highest point, the platform is accelerating downward.
⇒ N = mg – ma
But a = ω2A .....[In magnitude]
∴ N = mg – mω2A
Where, A = amplitude of motion
Given, m = 50 kg, frequency v = 2 s–1
∴ ω = 2πv = 4π rad/s
A = 5 cm = 5 × 10–2 m
∴ N = 50 × 9.8 – 50 × (4π)2 × 5×10–2
= 50[9.8 – 16π2 × 5 × 10–2]
= 50[9.8 – 7.89]
= 50 × 1.91
= 95.5 N
When the platform is at the lowest position of its oscillation,
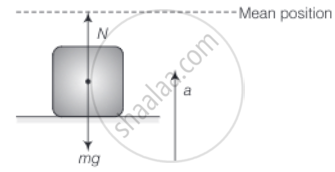
It is accelerating towards the mean position that is vertically upwards.
Writing the equation of motion
N – mg = ma = mω2A
or N = mg + mω2A
= m[g + ω2A]
Putting the data N = 50[9.8 + (4π)2 × 5 × 10–2]
= 50[9.8 + (12.56)2 × 5 × 10–2]
= 50[9.8 + 7.88]
= 50 × 17.68
= 884 N
Now, the machine reads the normal reaction. It is clear that
Maximum weight = 884 N ......(At lowest point)
Minimum weight = 955 N .....(At top point)
APPEARS IN
RELATED QUESTIONS
A copper metal cube has each side of length 1 m. The bottom edge of the cube is fixed and tangential force 4.2x108 N is applied to a top surface. Calculate the lateral displacement of the top surface if modulus of rigidity of copper is 14x1010 N/m2.
Which of the following example represent periodic motion?
An arrow released from a bow.
The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 m. If the piston moves with simple harmonic motion with an angular frequency of 200 rad/min, what is its maximum speed?
A person goes to bed at sharp 10.00 pm every day. Is it an example of periodic motion? If yes, what is the time period? If no, why?
A particle executes simple harmonic motion with a frequency v. The frequency with which the kinetic energy oscillates is
A particle moves in a circular path with a uniform speed. Its motion is
A particle is fastened at the end of a string and is whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
A spring stores 5 J of energy when stretched by 25 cm. It is kept vertical with the lower end fixed. A block fastened to its other end is made to undergo small oscillations. If the block makes 5 oscillations each second what is the mass of the block?
The string the spring and the pulley shown in figure are light. Find the time period of the mass m.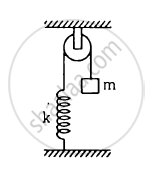
Find the time period of the motion of the particle shown in figure . Neglect the small effect of the bend near the bottom.
Find the number of oscillations performed per minute by a magnet is vibrating in the plane of a uniform field of 1.6 × 10-5 Wb/m2. The magnet has a moment of inertia 3 × 10-6 kg/m2 and magnetic moment 3 A m2.
The maximum speed of a particle executing S.H.M. is 10 m/s and maximum acceleration is 31.4 m/s2. Its periodic time is ______
Which of the following example represent periodic motion?
A freely suspended bar magnet displaced from its N-S direction and released.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
The rotation of the earth about its axis.
Which of the following example represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
A motion of an oscillating mercury column in a U-tube.
Show that the motion of a particle represented by y = sin ωt – cos ωt is simple harmonic with a period of 2π/ω.
The time period of a simple pendulum is T inside a lift when the lift is stationary. If the lift moves upwards with an acceleration `g/2`, the time period of the pendulum will be ______.
