Advertisements
Advertisements
Question
Consider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2° to the right with the vertical, the other pendulum makes an angle of 1° to the left of the vertical. What is the phase difference between the pendulums?
Advertisements
Solution
Consider the situations shown in the diagram (i) and (ii)
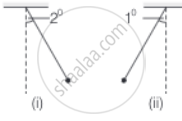
Assuming the two pendulums follow the following functions of their angular displacements
`θ_1 = θ_0 sin(ωt + phi_1)` .......(i)
And `θ_2 = θ_0 sin(ωt + phi_2)` .......(ii)
As it is given amplitude and time period are equal but phases being different.
Now, for the first pendulum at any time t
`θ_1 = + θ_0` .....[Right extreme]
From equation (i), we get
⇒ `θ_0 = θ_0 sin(ωt + phi_1)` or 1 = `sin(θt + phi_1)`
⇒ `sin pi/2 = sin(ωt + phi_1)`
or `(ωt + phi_1) = pi/2` ......(iii)
Similarly, at the same instant t for pendulum second, we have `θ_2 = - θ_0/2` where θ0 = 2° is the angular amplitude of the first pendulum. For the second pendulum, the angular displacement is one degree, therefore `θ_2 = θ_0/2` and a negative sign is taken to show for being left to mean position.
From equation (ii), then `- θ_0/2 = θ_0 sin(ωt + phi_2)`
⇒ `sin(ωt + phi_2) = - 1/2`
⇒ `(ωt + phi_2) = - pi/6 or (7pi)/6`
or `(ωt + phi_2) = - pi/6 or (7pi)/6` ......(iv)
From equations (iv) and (iii), the difference in phases
`(ωt + phi_2) - (ωt + phi_2) = (7pi)/6 - pi/2`
= `(7pi - 3pi)/6`
= `(4pi)/6`
Or `(phi_2 - phi_1) = (4pi)/6 = (2pi)/3` = 120°
APPEARS IN
RELATED QUESTIONS
The period of a conical pendulum in terms of its length (l), semi-vertical angle (θ) and acceleration due to gravity (g) is ______.
let us take the position of mass when the spring is unstretched as x = 0, and the direction from left to right as the positive direction of the x-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0), the mass is
(a) at the mean position,
(b) at the maximum stretched position, and
(c) at the maximum compressed position.
In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase?
Answer the following questions:
A time period of a particle in SHM depends on the force constant k and mass m of the particle: `T = 2pi sqrt(m/k)` A simple pendulum executes SHM approximately. Why then is the time
Answer the following questions:
The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than `2pisqrt(1/g)` Think of a qualitative argument to appreciate this result.
Answer the following questions:
A man with a wristwatch on his hand falls from the top of a tower. Does the watch give correct time during the free fall?
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?
Define practical simple pendulum
Show that motion of bob of the pendulum with small amplitude is linear S.H.M. Hence obtain an expression for its period. What are the factors on which its period depends?
Show that, under certain conditions, simple pendulum performs the linear simple harmonic motion.
If the particle starts its motion from mean position, the phase difference between displacement and acceleration is ______.
A simple pendulum has a time period of T1 when on the earth's surface and T2 when taken to a height R above the earth's surface, where R is the radius of the earth. The value of `"T"_2 // "T"_1` is ______.
The period of oscillation of a simple pendulum of constant length at the surface of the earth is T. Its time period inside mine will be ______.
The relation between acceleration and displacement of four particles are given below: Which one of the particles is executing simple harmonic motion?
The length of a second’s pendulum on the surface of earth is 1 m. What will be the length of a second’s pendulum on the moon?
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be:
A pendulum of mass m and length ℓ is suspended from the ceiling of a trolley which has a constant acceleration a in the horizontal direction as shown in the figure. Work done by the tension is ______.
(In the frame of the trolley)
