Advertisements
Advertisements
प्रश्न
Consider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2° to the right with the vertical, the other pendulum makes an angle of 1° to the left of the vertical. What is the phase difference between the pendulums?
Advertisements
उत्तर
Consider the situations shown in the diagram (i) and (ii)
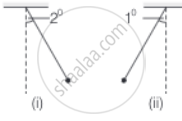
Assuming the two pendulums follow the following functions of their angular displacements
`θ_1 = θ_0 sin(ωt + phi_1)` .......(i)
And `θ_2 = θ_0 sin(ωt + phi_2)` .......(ii)
As it is given amplitude and time period are equal but phases being different.
Now, for the first pendulum at any time t
`θ_1 = + θ_0` .....[Right extreme]
From equation (i), we get
⇒ `θ_0 = θ_0 sin(ωt + phi_1)` or 1 = `sin(θt + phi_1)`
⇒ `sin pi/2 = sin(ωt + phi_1)`
or `(ωt + phi_1) = pi/2` ......(iii)
Similarly, at the same instant t for pendulum second, we have `θ_2 = - θ_0/2` where θ0 = 2° is the angular amplitude of the first pendulum. For the second pendulum, the angular displacement is one degree, therefore `θ_2 = θ_0/2` and a negative sign is taken to show for being left to mean position.
From equation (ii), then `- θ_0/2 = θ_0 sin(ωt + phi_2)`
⇒ `sin(ωt + phi_2) = - 1/2`
⇒ `(ωt + phi_2) = - pi/6 or (7pi)/6`
or `(ωt + phi_2) = - pi/6 or (7pi)/6` ......(iv)
From equations (iv) and (iii), the difference in phases
`(ωt + phi_2) - (ωt + phi_2) = (7pi)/6 - pi/2`
= `(7pi - 3pi)/6`
= `(4pi)/6`
Or `(phi_2 - phi_1) = (4pi)/6 = (2pi)/3` = 120°
APPEARS IN
संबंधित प्रश्न
When the length of a simple pendulum is decreased by 20 cm, the period changes by 10%. Find the original length of the pendulum.
The phase difference between displacement and acceleration of a particle performing S.H.M. is _______.
(A) `pi/2rad`
(B) π rad
(C) 2π rad
(D)`(3pi)/2rad`
let us take the position of mass when the spring is unstretched as x = 0, and the direction from left to right as the positive direction of the x-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0), the mass is
(a) at the mean position,
(b) at the maximum stretched position, and
(c) at the maximum compressed position.
In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase?
Answer the following questions:
The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than `2pisqrt(1/g)` Think of a qualitative argument to appreciate this result.
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?
A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t = 0. Determine the amplitude of the resulting oscillations in terms of the parameters ω, x0 and v0. [Hint: Start with the equation x = acos (ωt+θ) and note that the initial velocity is negative.]
A clock regulated by seconds pendulum, keeps correct time. During summer, length of pendulum increases to 1.005 m. How much will the clock gain or loose in one day?
(g = 9.8 m/s2 and π = 3.142)
Show that, under certain conditions, simple pendulum performs the linear simple harmonic motion.
If the particle starts its motion from mean position, the phase difference between displacement and acceleration is ______.
A simple pendulum has a time period of T1 when on the earth's surface and T2 when taken to a height R above the earth's surface, where R is the radius of the earth. The value of `"T"_2 // "T"_1` is ______.
When will the motion of a simple pendulum be simple harmonic?
The length of a second’s pendulum on the surface of earth is 1 m. What will be the length of a second’s pendulum on the moon?
A body of mass m is situated in a potential field U(x) = U0 (1 – cos αx) when U0 and α are constants. Find the time period of small oscillations.
A simple pendulum of time period 1s and length l is hung from a fixed support at O, such that the bob is at a distance H vertically above A on the ground (Figure). The amplitude is θ0. The string snaps at θ = θ0/2. Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume θo to be small so that sin θo = θo and cos θo = 1.
In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be:
A pendulum of mass m and length ℓ is suspended from the ceiling of a trolley which has a constant acceleration a in the horizontal direction as shown in the figure. Work done by the tension is ______.
(In the frame of the trolley)
A particle at the end of a spring executes simple harmonic motion with a period t1, while the corresponding period for another spring is t2. If the period of oscillation with the two springs in series is T, then ______.
If the mass of the bob in a simple pendulum is increased to thrice its original mass and its length is made half its original length, then the new time period of oscillation is `x/2` times its original time period. Then the value of x is ______.
