Advertisements
Advertisements
प्रश्न
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?
उत्तर १
The bob of the simple pendulum will experience the acceleration due to gravity and the centripetal acceleration provided by the circular motion of the car.
Acceleration due to gravity = g
Centripetal acceleration = `v^2/R`
Where,
v is the uniform speed of the car
R is the radius of the track
Effective acceleration (aeff) is given as:
`a_"eff" = sqrt(g^2 + (v^2/R)^2)`
Time period, `T = 2pi sqrt(1/a_"eff")`
Where, l is the length of the pendulum
:. Time period, `T = 2pi sqrt(1/(g^2 + v^4/R^2))`
उत्तर २
In this case, the bob of the pendulum is under the action of two accelerations.
1) Acceleration due to gravity 'g' acting vertically downwards.
2) Centripetal acceleration `a_c = v^2/R` acting along the horizontal direction.
:. Effective acceleration, `g' = sqrt(g^2 + a_c^2)` or `g' = sqrt(g^2 + v^4/R^2)`
Now time period, `T' = 2pi sqrt(1/g) = 2pi sqrt(1/(sqrt(g^2 + v^4/R62)))`
APPEARS IN
संबंधित प्रश्न
The period of a conical pendulum in terms of its length (l), semi-vertical angle (θ) and acceleration due to gravity (g) is:
If the metal bob of a simple pendulum is replaced by a wooden bob of the same size, then its time period will.....................
- increase
- remain same
- decrease
- first increase and then decrease.
When the length of a simple pendulum is decreased by 20 cm, the period changes by 10%. Find the original length of the pendulum.
The cylindrical piece of the cork of density of base area A and height h floats in a liquid of density `rho_1`. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
`T = 2pi sqrt((hrho)/(rho_1g)`
where ρ is the density of cork. (Ignore damping due to viscosity of the liquid).
A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t = 0. Determine the amplitude of the resulting oscillations in terms of the parameters ω, x0 and v0. [Hint: Start with the equation x = acos (ωt+θ) and note that the initial velocity is negative.]
A simple pendulum has a time period of T1 when on the earth's surface and T2 when taken to a height R above the earth's surface, where R is the radius of the earth. The value of `"T"_2 // "T"_1` is ______.
The relation between acceleration and displacement of four particles are given below: Which one of the particles is executing simple harmonic motion?
A particle executing S.H.M. has a maximum speed of 30 cm/s and a maximum acceleration of 60 cm/s2. The period of oscillation is ______.
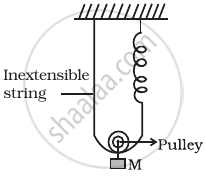
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
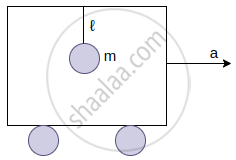
A pendulum of mass m and length ℓ is suspended from the ceiling of a trolley which has a constant acceleration a in the horizontal direction as shown in the figure. Work done by the tension is ______.
(In the frame of the trolley)