Advertisements
Advertisements
Question
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?
Solution 1
The bob of the simple pendulum will experience the acceleration due to gravity and the centripetal acceleration provided by the circular motion of the car.
Acceleration due to gravity = g
Centripetal acceleration = `v^2/R`
Where,
v is the uniform speed of the car
R is the radius of the track
Effective acceleration (aeff) is given as:
`a_"eff" = sqrt(g^2 + (v^2/R)^2)`
Time period, `T = 2pi sqrt(1/a_"eff")`
Where, l is the length of the pendulum
:. Time period, `T = 2pi sqrt(1/(g^2 + v^4/R^2))`
Solution 2
In this case, the bob of the pendulum is under the action of two accelerations.
1) Acceleration due to gravity 'g' acting vertically downwards.
2) Centripetal acceleration `a_c = v^2/R` acting along the horizontal direction.
:. Effective acceleration, `g' = sqrt(g^2 + a_c^2)` or `g' = sqrt(g^2 + v^4/R^2)`
Now time period, `T' = 2pi sqrt(1/g) = 2pi sqrt(1/(sqrt(g^2 + v^4/R62)))`
APPEARS IN
RELATED QUESTIONS
When the length of a simple pendulum is decreased by 20 cm, the period changes by 10%. Find the original length of the pendulum.
Answer the following questions:
A man with a wristwatch on his hand falls from the top of a tower. Does the watch give correct time during the free fall?
Show that, under certain conditions, simple pendulum performs the linear simple harmonic motion.
If the particle starts its motion from mean position, the phase difference between displacement and acceleration is ______.
A simple pendulum has a time period of T1 when on the earth's surface and T2 when taken to a height R above the earth's surface, where R is the radius of the earth. The value of `"T"_2 // "T"_1` is ______.
If the maximum velocity and acceleration of a particle executing SHM are equal in magnitude, the time period will be ______.
Which of the following statements is/are true for a simple harmonic oscillator?
- Force acting is directly proportional to displacement from the mean position and opposite to it.
- Motion is periodic.
- Acceleration of the oscillator is constant.
- The velocity is periodic.
When will the motion of a simple pendulum be simple harmonic?
Consider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2° to the right with the vertical, the other pendulum makes an angle of 1° to the left of the vertical. What is the phase difference between the pendulums?
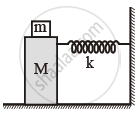
In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be: