Advertisements
Advertisements
प्रश्न
A body of mass m is situated in a potential field U(x) = U0 (1 – cos αx) when U0 and α are constants. Find the time period of small oscillations.
उत्तर
Given the potential energy associated with the field
U(x) = U0 (1 – cos αx) [∵ For conservative force f, we can write f = `(-du)/(dx)`] ......(i)
Now, Force F = `- (dU(x))/(dx)` .....[We have assumed the field to be conservative]
F = `- d/(dx) (U_0 - U_0 cos ax) = - U_0 a sin ax`
F = `- U_0 a^2x` [∵ For small oscillations ax is small, sin ax ≈ ax] ......(ii)
⇒ F ∝ (– x)
As, U0, a being constant.
∴ Motion is S.H.M for small oscillations.
The standard equation for S.H.M F = `- mω^2x` ......(iii)
Comparing equations (ii) and (iii), we get
`mω^2 = U_0a^2`
`ω^2 = (U_0a^2)/m` or `ω = sqrt((U_0a^2)/m)`
∴ Time period T = `(2pi)/ω = 2pi sqrt(m/(U_0a^2))`
APPEARS IN
संबंधित प्रश्न
When the length of a simple pendulum is decreased by 20 cm, the period changes by 10%. Find the original length of the pendulum.
Answer the following questions:
A man with a wristwatch on his hand falls from the top of a tower. Does the watch give correct time during the free fall?
Answer the following questions:
What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling under gravity?
If the maximum velocity and acceleration of a particle executing SHM are equal in magnitude, the time period will be ______.
The period of oscillation of a simple pendulum of constant length at the surface of the earth is T. Its time period inside mine will be ______.
Which of the following statements is/are true for a simple harmonic oscillator?
- Force acting is directly proportional to displacement from the mean position and opposite to it.
- Motion is periodic.
- Acceleration of the oscillator is constant.
- The velocity is periodic.
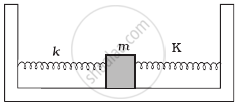
Two identical springs of spring constant K are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force
The length of a second’s pendulum on the surface of earth is 1 m. What will be the length of a second’s pendulum on the moon?
Consider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2° to the right with the vertical, the other pendulum makes an angle of 1° to the left of the vertical. What is the phase difference between the pendulums?
A particle at the end of a spring executes simple harmonic motion with a period t1, while the corresponding period for another spring is t2. If the period of oscillation with the two springs in series is T, then ______.
