Advertisements
Advertisements
प्रश्न
Which of the following statements is/are true for a simple harmonic oscillator?
- Force acting is directly proportional to displacement from the mean position and opposite to it.
- Motion is periodic.
- Acceleration of the oscillator is constant.
- The velocity is periodic.
Advertisements
उत्तर
a, b and d
Explanation:
Simple harmonic motion is a type of periodic motion or oscillation motion where the restoring force is directly proportional to the displacement and acts in the direction opposite to that of displacement. When the system is displaced from its equilibrium position, a restoring force that obeys Hooke’s law tends to restore the system to equilibrium. As a result, it accelerates and starts going back to the equilibrium position.
An oscillation follows simple harmonic motion if it fulfils the following two rules:
- Acceleration is always in the opposite direction to the displacement from the equilibrium position.
- Acceleration is proportional to the displacement from the equilibrium position.
Let us write the equation for the SHM x = a sin(ωt + `phi`)
Clearly, it is a periodic motion as it involves since function.
Let us find velocity of the particle, `v = (dx)/(dt)`
= `d/(dt) (a sin(ωt + phi))`
= `aω cos(ωt + phi)`
Velocity is also periodic because it is a cosine function.
Now let us find acceleration, `A = (dv)/(dt)`
= `(d^2x)/(dt^2)`
= `- aω^2 sin(ωt + phi)`
The acceleration is a sine function, hence cannot be constant.
⇒ `A = - (ω^2a) sin(ωt + phi) = - ω^2x`
Force, F = Mass × Acceleration
= mA
= – mω2x
Hence, force acting is directly proportional to displacement from the mean position and opposite to it.
APPEARS IN
संबंधित प्रश्न
The period of a conical pendulum in terms of its length (l), semi-vertical angle (θ) and acceleration due to gravity (g) is ______.
If the metal bob of a simple pendulum is replaced by a wooden bob of the same size, then its time period will.....................
- increase
- remain same
- decrease
- first increase and then decrease.
When the length of a simple pendulum is decreased by 20 cm, the period changes by 10%. Find the original length of the pendulum.
let us take the position of mass when the spring is unstretched as x = 0, and the direction from left to right as the positive direction of the x-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0), the mass is
(a) at the mean position,
(b) at the maximum stretched position, and
(c) at the maximum compressed position.
In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase?
Answer the following questions:
The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than `2pisqrt(1/g)` Think of a qualitative argument to appreciate this result.
Answer the following questions:
What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling under gravity?
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?
A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t = 0. Determine the amplitude of the resulting oscillations in terms of the parameters ω, x0 and v0. [Hint: Start with the equation x = acos (ωt+θ) and note that the initial velocity is negative.]
Define practical simple pendulum
Show that motion of bob of the pendulum with small amplitude is linear S.H.M. Hence obtain an expression for its period. What are the factors on which its period depends?
Show that, under certain conditions, simple pendulum performs the linear simple harmonic motion.
A simple pendulum has a time period of T1 when on the earth's surface and T2 when taken to a height R above the earth's surface, where R is the radius of the earth. The value of `"T"_2 // "T"_1` is ______.
The period of oscillation of a simple pendulum of constant length at the surface of the earth is T. Its time period inside mine will be ______.
When will the motion of a simple pendulum be simple harmonic?
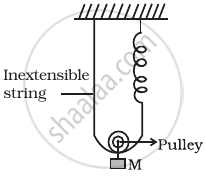
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
Consider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2° to the right with the vertical, the other pendulum makes an angle of 1° to the left of the vertical. What is the phase difference between the pendulums?
In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be:
A particle at the end of a spring executes simple harmonic motion with a period t1, while the corresponding period for another spring is t2. If the period of oscillation with the two springs in series is T, then ______.
If the mass of the bob in a simple pendulum is increased to thrice its original mass and its length is made half its original length, then the new time period of oscillation is `x/2` times its original time period. Then the value of x is ______.
