Advertisements
Advertisements
प्रश्न
A clock regulated by seconds pendulum, keeps correct time. During summer, length of pendulum increases to 1.005 m. How much will the clock gain or loose in one day?
(g = 9.8 m/s2 and π = 3.142)
उत्तर
Given: L = 1.005 m, g = 9.8 m/s2
To find: Loss in period (ΔT)
Formula: `T=2pisqrt(L/g)`
`T=2xx3.14xxsqrt(1.005/9.8)`
`=2.012 s`
The period of a seconds pendulum is 2 second.
Hence, the given pendulum clock will lose 0.012s in 2.012s (during summer).
Loss in period per day
`ΔT=(24xx3600xx0.012)/2.012`
`DeltaT=515.3s`
The clock will gain or lose 515.3 s in one day.
APPEARS IN
संबंधित प्रश्न
The period of a conical pendulum in terms of its length (l), semi-vertical angle (θ) and acceleration due to gravity (g) is:
When the length of a simple pendulum is decreased by 20 cm, the period changes by 10%. Find the original length of the pendulum.
The phase difference between displacement and acceleration of a particle performing S.H.M. is _______.
(A) `pi/2rad`
(B) π rad
(C) 2π rad
(D)`(3pi)/2rad`
A spring having with a spring constant 1200 N m–1 is mounted on a horizontal table as shown in Fig. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.

Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
The acceleration due to gravity on the surface of moon is 1.7 ms–2. What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is 3.5 s? (g on the surface of earth is 9.8 ms–2)
Answer the following questions:
The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than `2pisqrt(1/g)` Think of a qualitative argument to appreciate this result.
Answer the following questions:
What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling under gravity?
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?
Show that motion of bob of the pendulum with small amplitude is linear S.H.M. Hence obtain an expression for its period. What are the factors on which its period depends?
Show that, under certain conditions, simple pendulum performs the linear simple harmonic motion.
If the particle starts its motion from mean position, the phase difference between displacement and acceleration is ______.
A simple pendulum has a time period of T1 when on the earth's surface and T2 when taken to a height R above the earth's surface, where R is the radius of the earth. The value of `"T"_2 // "T"_1` is ______.
The period of oscillation of a simple pendulum of constant length at the surface of the earth is T. Its time period inside mine will be ______.
The relation between acceleration and displacement of four particles are given below: Which one of the particles is executing simple harmonic motion?
Which of the following statements is/are true for a simple harmonic oscillator?
- Force acting is directly proportional to displacement from the mean position and opposite to it.
- Motion is periodic.
- Acceleration of the oscillator is constant.
- The velocity is periodic.
Two identical springs of spring constant K are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force
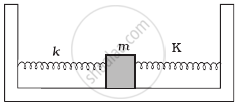
When will the motion of a simple pendulum be simple harmonic?
A body of mass m is situated in a potential field U(x) = U0 (1 – cos αx) when U0 and α are constants. Find the time period of small oscillations.
A cylindrical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that the log would execute S.H.M. with a time period. `T = 2πsqrt(m/(Apg))` where m is mass of the body and ρ is density of the liquid.
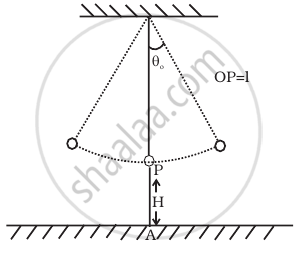
A simple pendulum of time period 1s and length l is hung from a fixed support at O, such that the bob is at a distance H vertically above A on the ground (Figure). The amplitude is θ0. The string snaps at θ = θ0/2. Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume θo to be small so that sin θo = θo and cos θo = 1.
A particle at the end of a spring executes simple harmonic motion with a period t1, while the corresponding period for another spring is t2. If the period of oscillation with the two springs in series is T, then ______.
