Advertisements
Advertisements
प्रश्न
The length of a second’s pendulum on the surface of earth is 1 m. What will be the length of a second’s pendulum on the moon?
उत्तर
A second's pendulum means a simple pendulum having a time period T = 2 s.
For a simple pendulum, T = `2pisqrt(l/g)`
Where, `l` = Length of the pendulum
And g = Acceleration due to gravity on surface of the earth
`T_e = 2pisqrt(l_e/g_e)` .......(i)
On the surface of the moon, `T_m = 2pisqrt(K_m/g_m)` ......(ii)
∴ `T_e/T_m = (2pi)/(2pi) sqrt(l_e/g_e) xx sqrt(g_m/l_m)`
Te = Tm to maintain the second pendulum time period.
∴ 1 = `sqrt(l_e/l_m xx g_m/g_e)` ......(iii)
But the acceleration due to gravity on the moon is 1/6 of the acceleration due to gravity on earth,
i.e., `g_m = g_e/6`
Squaring equation (iii) and putting this value.
1 = `l_e/l_m xx (g_e/6)/g_e = l_e/l_m xx 1/6`
⇒ `l_e/(6l_m)` = 1
⇒ `6l_m = l_e`
⇒ `l_m = 1/6 l_e = 1/6 xx 1 = 1/6 m`
APPEARS IN
संबंधित प्रश्न
The period of a conical pendulum in terms of its length (l), semi-vertical angle (θ) and acceleration due to gravity (g) is:
When the length of a simple pendulum is decreased by 20 cm, the period changes by 10%. Find the original length of the pendulum.
The acceleration due to gravity on the surface of moon is 1.7 ms–2. What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is 3.5 s? (g on the surface of earth is 9.8 ms–2)
Answer the following questions:
A time period of a particle in SHM depends on the force constant k and mass m of the particle: `T = 2pi sqrt(m/k)` A simple pendulum executes SHM approximately. Why then is the time
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?
If the particle starts its motion from mean position, the phase difference between displacement and acceleration is ______.
The relation between acceleration and displacement of four particles are given below: Which one of the particles is executing simple harmonic motion?
A particle executing S.H.M. has a maximum speed of 30 cm/s and a maximum acceleration of 60 cm/s2. The period of oscillation is ______.
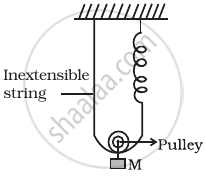
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
A simple pendulum of time period 1s and length l is hung from a fixed support at O, such that the bob is at a distance H vertically above A on the ground (Figure). The amplitude is θ0. The string snaps at θ = θ0/2. Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume θo to be small so that sin θo = θo and cos θo = 1.