Advertisements
Advertisements
प्रश्न
The length of a second’s pendulum on the surface of earth is 1 m. What will be the length of a second’s pendulum on the moon?
उत्तर
A second's pendulum means a simple pendulum having a time period T = 2 s.
For a simple pendulum, T = `2pisqrt(l/g)`
Where, `l` = Length of the pendulum
And g = Acceleration due to gravity on surface of the earth
`T_e = 2pisqrt(l_e/g_e)` .......(i)
On the surface of the moon, `T_m = 2pisqrt(K_m/g_m)` ......(ii)
∴ `T_e/T_m = (2pi)/(2pi) sqrt(l_e/g_e) xx sqrt(g_m/l_m)`
Te = Tm to maintain the second pendulum time period.
∴ 1 = `sqrt(l_e/l_m xx g_m/g_e)` ......(iii)
But the acceleration due to gravity on the moon is 1/6 of the acceleration due to gravity on earth,
i.e., `g_m = g_e/6`
Squaring equation (iii) and putting this value.
1 = `l_e/l_m xx (g_e/6)/g_e = l_e/l_m xx 1/6`
⇒ `l_e/(6l_m)` = 1
⇒ `6l_m = l_e`
⇒ `l_m = 1/6 l_e = 1/6 xx 1 = 1/6 m`
APPEARS IN
संबंधित प्रश्न
The period of a conical pendulum in terms of its length (l), semi-vertical angle (θ) and acceleration due to gravity (g) is:
A spring having with a spring constant 1200 N m–1 is mounted on a horizontal table as shown in Fig. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.

Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
Answer the following questions:
The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than `2pisqrt(1/g)` Think of a qualitative argument to appreciate this result.
The cylindrical piece of the cork of density of base area A and height h floats in a liquid of density `rho_1`. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
`T = 2pi sqrt((hrho)/(rho_1g)`
where ρ is the density of cork. (Ignore damping due to viscosity of the liquid).
A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t = 0. Determine the amplitude of the resulting oscillations in terms of the parameters ω, x0 and v0. [Hint: Start with the equation x = acos (ωt+θ) and note that the initial velocity is negative.]
A simple pendulum has a time period of T1 when on the earth's surface and T2 when taken to a height R above the earth's surface, where R is the radius of the earth. The value of `"T"_2 // "T"_1` is ______.
The period of oscillation of a simple pendulum of constant length at the surface of the earth is T. Its time period inside mine will be ______.
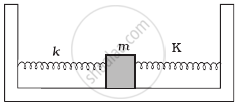
Two identical springs of spring constant K are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force
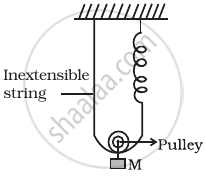
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
A particle at the end of a spring executes simple harmonic motion with a period t1, while the corresponding period for another spring is t2. If the period of oscillation with the two springs in series is T, then ______.
