Advertisements
Advertisements
प्रश्न
Answer the following questions:
The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than `2pisqrt(1/g)` Think of a qualitative argument to appreciate this result.
उत्तर १
In the case of a simple pendulum, the restoring force acting on the bob of the pendulum is given as:
F = –mg sinθ
Where,
F = Restoring force
m = Mass of the bob
g = Acceleration due to gravity
θ = Angle of displacement
For small θ, sinθ = θ
For large θ, sinθ is greater than θ.
This decreases the effective value of g.
Hence, the time period increases as:
`T = 2pi sqrt(1/g)`
Where, l is the length of the simple pendulum
उत्तर २
The restoring force for the bob of the pendulum is given by
`F = -mg sintheta`
if `theta` is small thensin `theta = theta = y/l` `:. F = -(mg)/l y`
i.e the motion is simple harmonic and time period is` T = 2pi sqrt(1/g)`
Clearly, the above formula is obtained only if we apply the approximation `sin theta ~~ theta`
For large angles this approximation is not valid and T is greater than `2pi sqrt(1/g)`
APPEARS IN
संबंधित प्रश्न
The phase difference between displacement and acceleration of a particle performing S.H.M. is _______.
(A) `pi/2rad`
(B) π rad
(C) 2π rad
(D)`(3pi)/2rad`
The acceleration due to gravity on the surface of moon is 1.7 ms–2. What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is 3.5 s? (g on the surface of earth is 9.8 ms–2)
Answer the following questions:
A man with a wristwatch on his hand falls from the top of a tower. Does the watch give correct time during the free fall?
Show that, under certain conditions, simple pendulum performs the linear simple harmonic motion.
If the particle starts its motion from mean position, the phase difference between displacement and acceleration is ______.
The period of oscillation of a simple pendulum of constant length at the surface of the earth is T. Its time period inside mine will be ______.
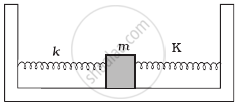
Two identical springs of spring constant K are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force
The length of a second’s pendulum on the surface of earth is 1 m. What will be the length of a second’s pendulum on the moon?
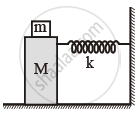
In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be:
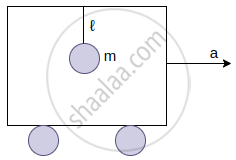
A pendulum of mass m and length ℓ is suspended from the ceiling of a trolley which has a constant acceleration a in the horizontal direction as shown in the figure. Work done by the tension is ______.
(In the frame of the trolley)