Advertisements
Advertisements
Question
Answer the following questions:
The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than `2pisqrt(1/g)` Think of a qualitative argument to appreciate this result.
Solution 1
In the case of a simple pendulum, the restoring force acting on the bob of the pendulum is given as:
F = –mg sinθ
Where,
F = Restoring force
m = Mass of the bob
g = Acceleration due to gravity
θ = Angle of displacement
For small θ, sinθ = θ
For large θ, sinθ is greater than θ.
This decreases the effective value of g.
Hence, the time period increases as:
`T = 2pi sqrt(1/g)`
Where, l is the length of the simple pendulum
Solution 2
The restoring force for the bob of the pendulum is given by
`F = -mg sintheta`
if `theta` is small thensin `theta = theta = y/l` `:. F = -(mg)/l y`
i.e the motion is simple harmonic and time period is` T = 2pi sqrt(1/g)`
Clearly, the above formula is obtained only if we apply the approximation `sin theta ~~ theta`
For large angles this approximation is not valid and T is greater than `2pi sqrt(1/g)`
APPEARS IN
RELATED QUESTIONS
When the length of a simple pendulum is decreased by 20 cm, the period changes by 10%. Find the original length of the pendulum.
Answer the following questions:
A time period of a particle in SHM depends on the force constant k and mass m of the particle: `T = 2pi sqrt(m/k)` A simple pendulum executes SHM approximately. Why then is the time
Answer the following questions:
A man with a wristwatch on his hand falls from the top of a tower. Does the watch give correct time during the free fall?
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?
A simple pendulum has a time period of T1 when on the earth's surface and T2 when taken to a height R above the earth's surface, where R is the radius of the earth. The value of `"T"_2 // "T"_1` is ______.
A particle executing S.H.M. has a maximum speed of 30 cm/s and a maximum acceleration of 60 cm/s2. The period of oscillation is ______.
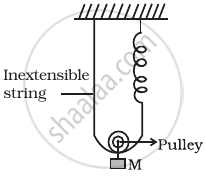
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
A body of mass m is situated in a potential field U(x) = U0 (1 – cos αx) when U0 and α are constants. Find the time period of small oscillations.
A tunnel is dug through the centre of the Earth. Show that a body of mass ‘m’ when dropped from rest from one end of the tunnel will execute simple harmonic motion.
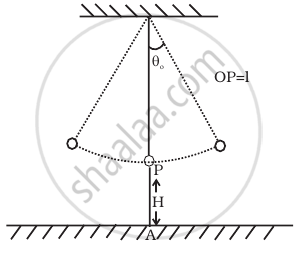
A simple pendulum of time period 1s and length l is hung from a fixed support at O, such that the bob is at a distance H vertically above A on the ground (Figure). The amplitude is θ0. The string snaps at θ = θ0/2. Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume θo to be small so that sin θo = θo and cos θo = 1.