Advertisements
Advertisements
Question
A particle executing S.H.M. has a maximum speed of 30 cm/s and a maximum acceleration of 60 cm/s2. The period of oscillation is ______.
Options
πs.
`π/2` s.
2π s.
`π/t` s.
Solution
A particle executing S.H.M. has a maximum speed of 30 cm/s and a maximum acceleration of 60 cm/s2. The period of oscillation is πs.
Explanation:
Let the equation of an SHM is represented by y = a sin ωt
v = `(dy)/(dt)` = a ωcos ωt
⇒ (v)max = aω = 30 ......(i)
Acceleration (A) = `(dx^2)/(dt^2)` = – aω2 sinωt
Amax = ω2a = 60 ......(ii)
In equations (i) and (ii), we get ω(ωa) = 60
⇒ ω(30) = 60
⇒ ω = 2 rad/s
⇒ `(2pi)/T` = 2 rad/s
⇒ T = π sec
APPEARS IN
RELATED QUESTIONS
A spring having with a spring constant 1200 N m–1 is mounted on a horizontal table as shown in Fig. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.

Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
let us take the position of mass when the spring is unstretched as x = 0, and the direction from left to right as the positive direction of the x-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0), the mass is
(a) at the mean position,
(b) at the maximum stretched position, and
(c) at the maximum compressed position.
In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase?
Answer the following questions:
The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than `2pisqrt(1/g)` Think of a qualitative argument to appreciate this result.
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?
Show that, under certain conditions, simple pendulum performs the linear simple harmonic motion.
If the particle starts its motion from mean position, the phase difference between displacement and acceleration is ______.
Two identical springs of spring constant K are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force
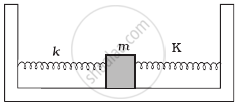
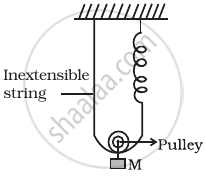
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
A tunnel is dug through the centre of the Earth. Show that a body of mass ‘m’ when dropped from rest from one end of the tunnel will execute simple harmonic motion.
A particle at the end of a spring executes simple harmonic motion with a period t1, while the corresponding period for another spring is t2. If the period of oscillation with the two springs in series is T, then ______.
