Advertisements
Advertisements
Question
A spring having with a spring constant 1200 N m–1 is mounted on a horizontal table as shown in Fig. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.
Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
Advertisements
Solution 1
Spring constant, k = 1200 N m–1
Mass, m = 3 kg
Displacement, A = 2.0 cm = 0.02 cm
(i) Frequency of oscillation v, is given by the relation:
`v = 1/T = 1/(2pi) sqrt(k/m)`
Where, T is the time period
`:. v = 1/(2xx3.14) sqrt(1200/3) = 3.18 "m/s"`
Hence, the frequency of oscillations is 3.18 cycles per second.
ii) Maximum acceleration (a) is given by the relation:
a = ω2 A
Where
ω = Angular frequency = `sqrt(k/m)`
A = Maximum displacement
`:. a = k/m A = (1200xx0.02)/(3) = 8 ms^(-2)`
Hence, the maximum acceleration of the mass is 8.0 m/s2
iii) Maximum velocity, vmax = Aω
`= A sqrt(k/m) = 0.02 xx sqrt(1200/3) = 0.4 "m/s"`
Hence, the maximum velocity of the mass is 0.4 m/s.
Solution 2
K = 1200 `Mn^(-1)`; m = 3.0 kg, a= 2.0 cm = 0.02 m
i) Frequency, `v = 1/T = 1/(2pi) sqrt(k/m) = 1/(2xx3.14) sqrt(1200/3) = 3.2 s^(-1)`
ii) Acceleration, A = `omega^2` `" " y = k/m y`
Acceleration will be maximum when y is maximum i.e y = q
:. max acceleration,` A_"max" = (ka)/m =(1200xx0.02)/3 = 8 ms^(-2)`
iii) Max speed of the mass will be when it is passing throught mean position
`V_"max" = aomega = sqrt(k/m) = 0.02 xx sqrt(1200/3) = 0.4 ms^(-1)`
APPEARS IN
RELATED QUESTIONS
When the length of a simple pendulum is decreased by 20 cm, the period changes by 10%. Find the original length of the pendulum.
The acceleration due to gravity on the surface of moon is 1.7 ms–2. What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is 3.5 s? (g on the surface of earth is 9.8 ms–2)
Answer the following questions:
The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than `2pisqrt(1/g)` Think of a qualitative argument to appreciate this result.
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?
The cylindrical piece of the cork of density of base area A and height h floats in a liquid of density `rho_1`. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
`T = 2pi sqrt((hrho)/(rho_1g)`
where ρ is the density of cork. (Ignore damping due to viscosity of the liquid).
A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t = 0. Determine the amplitude of the resulting oscillations in terms of the parameters ω, x0 and v0. [Hint: Start with the equation x = acos (ωt+θ) and note that the initial velocity is negative.]
A clock regulated by seconds pendulum, keeps correct time. During summer, length of pendulum increases to 1.005 m. How much will the clock gain or loose in one day?
(g = 9.8 m/s2 and π = 3.142)
Define practical simple pendulum
A simple pendulum has a time period of T1 when on the earth's surface and T2 when taken to a height R above the earth's surface, where R is the radius of the earth. The value of `"T"_2 // "T"_1` is ______.
If the maximum velocity and acceleration of a particle executing SHM are equal in magnitude, the time period will be ______.
The period of oscillation of a simple pendulum of constant length at the surface of the earth is T. Its time period inside mine will be ______.
When will the motion of a simple pendulum be simple harmonic?
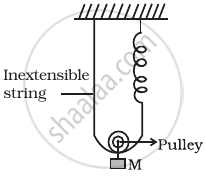
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
A body of mass m is situated in a potential field U(x) = U0 (1 – cos αx) when U0 and α are constants. Find the time period of small oscillations.
Consider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2° to the right with the vertical, the other pendulum makes an angle of 1° to the left of the vertical. What is the phase difference between the pendulums?
A cylindrical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that the log would execute S.H.M. with a time period. `T = 2πsqrt(m/(Apg))` where m is mass of the body and ρ is density of the liquid.
In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be:
A pendulum of mass m and length ℓ is suspended from the ceiling of a trolley which has a constant acceleration a in the horizontal direction as shown in the figure. Work done by the tension is ______.
(In the frame of the trolley)
If the mass of the bob in a simple pendulum is increased to thrice its original mass and its length is made half its original length, then the new time period of oscillation is `x/2` times its original time period. Then the value of x is ______.
