Advertisements
Advertisements
Question
The relation between acceleration and displacement of four particles are given below: Which one of the particles is executing simple harmonic motion?
Options
ax = + 2x.
ax = + 2x2.
ax = – 2x2.
ax = – 2x.
Solution
ax = – 2x.
Explanation:
In simple harmonic motion, acceleration is proportional and opposite to displacement. Applying the equation of motion
F = ma
a = − ω2x
a ∝− x
Hence − 2x represents SHM.
APPEARS IN
RELATED QUESTIONS
The period of a conical pendulum in terms of its length (l), semi-vertical angle (θ) and acceleration due to gravity (g) is:
Answer the following questions:
A time period of a particle in SHM depends on the force constant k and mass m of the particle: `T = 2pi sqrt(m/k)` A simple pendulum executes SHM approximately. Why then is the time
Answer the following questions:
A man with a wristwatch on his hand falls from the top of a tower. Does the watch give correct time during the free fall?
A clock regulated by seconds pendulum, keeps correct time. During summer, length of pendulum increases to 1.005 m. How much will the clock gain or loose in one day?
(g = 9.8 m/s2 and π = 3.142)
Show that motion of bob of the pendulum with small amplitude is linear S.H.M. Hence obtain an expression for its period. What are the factors on which its period depends?
A particle executing S.H.M. has a maximum speed of 30 cm/s and a maximum acceleration of 60 cm/s2. The period of oscillation is ______.
Which of the following statements is/are true for a simple harmonic oscillator?
- Force acting is directly proportional to displacement from the mean position and opposite to it.
- Motion is periodic.
- Acceleration of the oscillator is constant.
- The velocity is periodic.
Consider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2° to the right with the vertical, the other pendulum makes an angle of 1° to the left of the vertical. What is the phase difference between the pendulums?
A tunnel is dug through the centre of the Earth. Show that a body of mass ‘m’ when dropped from rest from one end of the tunnel will execute simple harmonic motion.
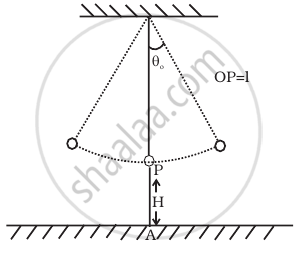
A simple pendulum of time period 1s and length l is hung from a fixed support at O, such that the bob is at a distance H vertically above A on the ground (Figure). The amplitude is θ0. The string snaps at θ = θ0/2. Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume θo to be small so that sin θo = θo and cos θo = 1.