Advertisements
Advertisements
प्रश्न
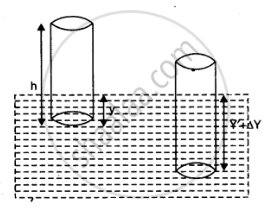
The cylindrical piece of the cork of density of base area A and height h floats in a liquid of density `rho_1`. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
`T = 2pi sqrt((hrho)/(rho_1g)`
where ρ is the density of cork. (Ignore damping due to viscosity of the liquid).
उत्तर १
Base area of the cork = A
Height of the cork = h
Density of the liquid = `rho_1`
Density of the cork = ρ
In equilibrium:
Weight of the cork = Weight of the liquid displaced by the floating cork
Let the cork be depressed slightly by x. As a result, some extra water of a certain volume is displaced. Hence, an extra up-thrust acts upward and provides the restoring force to the cork.
Up-thrust = Restoring force, F = Weight of the extra water displaced
F = –(Volume × Density × g)
Volume = Area × Distance through which the cork is depressed
Volume = Ax
∴ F = – A x `rho_1` g … (i)
According to the force law:
F = kx
`k = F/x`
Where, k is a constant
`k = F/x = -Arho_1g` ...(ii)
The time period of the oscillations of the cork:
`T = 2pi sqrt(m/k)` ...(iii)
Where
m = Mass of the cork
= Volume of the cork × Density
= Base area of the cork × Height of the cork × Density of the cork
= Ahρ
Hence, the expression for the time period becomes:
`T = 2pi sqrt((Ahrho)/(Arho_1g)) = 2 pi sqrt((hrho)/(rho_1g)`
उत्तर २
Say, initially in equilibrium, y height of cylinder is inside the liquid. Then,
Weight of the cylinder = upthrust due to liquid displaced
`:. Ahrhog = Ayrho_1g`
When the cork cylinder is depressed slightly by `triangle y` and released, a restoring force, equal to additional upthrust, act on it. The restoring force is
`F = A(y + triangle y) rho_1 g - Ayrho_1g = Arho_1g triangle y`
:. Acceleration, `a = F/m = (Arho_1g triangle y)/(Ahrho) = (rho_1g)/(hrho). triangle y ` and the acceleration is directed in a direction opposite to `triangle y`. Obviously, as `a prop - triangle y`, the motion of cork cylinder is SHM, whose time period is given by
`T = 2pi sqrt("displacement"/"accelertion")`
`=2pi sqrt((triangle y)/a)`
`= 2pi sqrt((hrho)/(rho_1g))`
APPEARS IN
संबंधित प्रश्न
The period of a conical pendulum in terms of its length (l), semi-vertical angle (θ) and acceleration due to gravity (g) is:
When the length of a simple pendulum is decreased by 20 cm, the period changes by 10%. Find the original length of the pendulum.
The phase difference between displacement and acceleration of a particle performing S.H.M. is _______.
(A) `pi/2rad`
(B) π rad
(C) 2π rad
(D)`(3pi)/2rad`
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?
The period of oscillation of a simple pendulum of constant length at the surface of the earth is T. Its time period inside mine will be ______.
Which of the following statements is/are true for a simple harmonic oscillator?
- Force acting is directly proportional to displacement from the mean position and opposite to it.
- Motion is periodic.
- Acceleration of the oscillator is constant.
- The velocity is periodic.
When will the motion of a simple pendulum be simple harmonic?
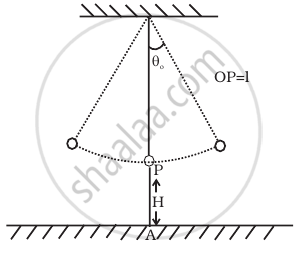
A simple pendulum of time period 1s and length l is hung from a fixed support at O, such that the bob is at a distance H vertically above A on the ground (Figure). The amplitude is θ0. The string snaps at θ = θ0/2. Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume θo to be small so that sin θo = θo and cos θo = 1.
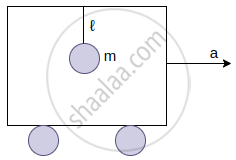
A pendulum of mass m and length ℓ is suspended from the ceiling of a trolley which has a constant acceleration a in the horizontal direction as shown in the figure. Work done by the tension is ______.
(In the frame of the trolley)
A particle at the end of a spring executes simple harmonic motion with a period t1, while the corresponding period for another spring is t2. If the period of oscillation with the two springs in series is T, then ______.
