Advertisements
Advertisements
प्रश्न
When will the motion of a simple pendulum be simple harmonic?
उत्तर
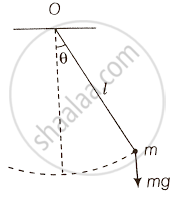
Simple pendulum performs angular S.H.M. Consider the bob of a simple pendulum is displaced through an angle θ shown. Q
The restoring torque about the fixed point O is τ = mgl sinθ
If θ is the small angle in radians, then sin θ = 0
⇒ mglθ
In vector form τ ∝ θ
Hence, the motion of a simple pendulum is SHM for small angles of oscillations.
APPEARS IN
संबंधित प्रश्न
The period of a conical pendulum in terms of its length (l), semi-vertical angle (θ) and acceleration due to gravity (g) is:
When the length of a simple pendulum is decreased by 20 cm, the period changes by 10%. Find the original length of the pendulum.
let us take the position of mass when the spring is unstretched as x = 0, and the direction from left to right as the positive direction of the x-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0), the mass is
(a) at the mean position,
(b) at the maximum stretched position, and
(c) at the maximum compressed position.
In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase?
The acceleration due to gravity on the surface of moon is 1.7 ms–2. What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is 3.5 s? (g on the surface of earth is 9.8 ms–2)
The cylindrical piece of the cork of density of base area A and height h floats in a liquid of density `rho_1`. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
`T = 2pi sqrt((hrho)/(rho_1g)`
where ρ is the density of cork. (Ignore damping due to viscosity of the liquid).
A clock regulated by seconds pendulum, keeps correct time. During summer, length of pendulum increases to 1.005 m. How much will the clock gain or loose in one day?
(g = 9.8 m/s2 and π = 3.142)
If the maximum velocity and acceleration of a particle executing SHM are equal in magnitude, the time period will be ______.
A particle executing S.H.M. has a maximum speed of 30 cm/s and a maximum acceleration of 60 cm/s2. The period of oscillation is ______.
Consider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2° to the right with the vertical, the other pendulum makes an angle of 1° to the left of the vertical. What is the phase difference between the pendulums?
In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be: