Advertisements
Advertisements
Question
Show that the motion of a particle represented by y = sin ωt – cos ωt is simple harmonic with a period of 2π/ω.
Solution
The given equation is in the form of a combination of two harmonic functions. We can write this equation in the form of a single harmonic (sine or cosine) function.
We have displacement function: `y = sin ωt - cos ωt`
`y = sqrt(2) (1/sqrt(2) * sin ωt - 1/sqrt(2) * cos ωt)`
= `sqrt(2)[cos (pi/4) * sin ωt - sin(pi/4) * cos ωt]`
= `sqrt(2) [sin (ωt - pi/4) = sqrt(2) [sin (ωt - pi/4)]]`
⇒ `y = sqrt(2) sin (ωt - pi/4)`
Comparing with the standard equation of S.H.M
`y = a sin(ωt + phi)` we get angular frequency of S.H.M, ω = `(2pi)/T` ⇒ `T = (2pi)/ω`
Hence the function represents S.H.M with a period T = 2π/ω.
APPEARS IN
RELATED QUESTIONS
A seconds pendulum is suspended in an elevator moving with constant speed in downward direction. The periodic time (T) of that pendulum is _______.
Answer in brief:
Derive an expression for the period of motion of a simple pendulum. On which factors does it depend?
A particle is fastened at the end of a string and is whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
A spring stores 5 J of energy when stretched by 25 cm. It is kept vertical with the lower end fixed. A block fastened to its other end is made to undergo small oscillations. If the block makes 5 oscillations each second what is the mass of the block?
The string the spring and the pulley shown in figure are light. Find the time period of the mass m.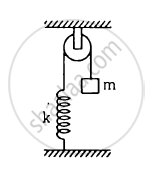
Find the time period of small oscillations of the following systems. (a) A metre stick suspended through the 20 cm mark. (b) A ring of mass m and radius r suspended through a point on its periphery. (c) A uniform square plate of edge a suspended through a corner. (d) A uniform disc of mass m and radius r suspended through a point r/2 away from the centre.
Which of the following example represent periodic motion?
A swimmer completing one (return) trip from one bank of a river to the other and back.
Which of the following example represent periodic motion?
A hydrogen molecule rotating about its center of mass.
A simple pendulum of frequency n falls freely under gravity from a certain height from the ground level. Its frequency of oscillation.
When a particle executes Simple Harmonic Motion, the nature of the graph of velocity as a function of displacement will be ______.
