Advertisements
Advertisements
प्रश्न
The total mechanical energy of a spring-mass system in simple harmonic motion is \[E = \frac{1}{2}m \omega^2 A^2 .\] Suppose the oscillating particle is replaced by another particle of double the mass while the amplitude A remains the same. The new mechanical energy will
पर्याय
become 2E
become E/2
become \[\sqrt{2}E\]
remain E
उत्तर
remain E
Mechanical energy (E) of a spring-mass system in simple harmonic motion is given by, \[E_{} = \frac{1}{2}m \omega^2 A^2\]
where m is mass of body, and \[\omega\] is angular frequency.
Let m1 be the mass of the other particle and ω1 be its angular frequency.
New angular frequency ω1 is given by,\[\omega_1 = \sqrt{\frac{k}{m_1}} = \sqrt{\frac{k}{2m}} ( m_1 = 2m)\]
New energy E1 is given as,
\[E_1 = \frac{1}{2} m_1 \omega_1^2 A^2 \]
\[ = \frac{1}{2}(2m)(\sqrt{\frac{k}{2m}} )^2 A^2 \]
\[ = \frac{1}{2}m \omega^2 A^2 = E\]
APPEARS IN
संबंधित प्रश्न
A seconds pendulum is suspended in an elevator moving with constant speed in downward direction. The periodic time (T) of that pendulum is _______.
The periodic time of a linear harmonic oscillator is 2π second, with maximum displacement of 1 cm. If the particle starts from extreme position, find the displacement of the particle after π/3 seconds.
A copper metal cube has each side of length 1 m. The bottom edge of the cube is fixed and tangential force 4.2x108 N is applied to a top surface. Calculate the lateral displacement of the top surface if modulus of rigidity of copper is 14x1010 N/m2.
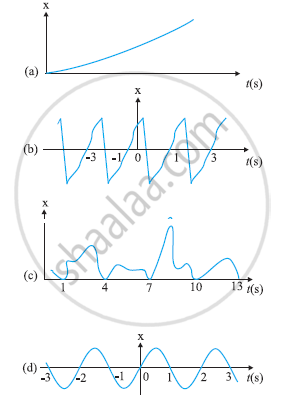
Figure depicts four x-t plots for linear motion of a particle. Which of the plots represent periodic motion? What is the period of motion (in case of periodic motion)?
The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 m. If the piston moves with simple harmonic motion with an angular frequency of 200 rad/min, what is its maximum speed?
The length of the second’s pendulum in a clock is increased to 4 times its initial length. Calculate the number of oscillations completed by the new pendulum in one minute.
A particle executes simple harmonic motion under the restoring force provided by a spring. The time period is T. If the spring is divided in two equal parts and one part is used to continue the simple harmonic motion, the time period will
A particle moves in a circular path with a uniform speed. Its motion is
A particle is fastened at the end of a string and is whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
The position, velocity and acceleration of a particle executing simple harmonic motion are found to have magnitude 2 cm, 1 m s−1 and 10 m s−2 at a certain instant. Find the amplitude and the time period of the motion.
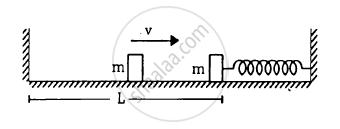
The left block in figure moves at a speed v towards the right block placed in equilibrium. All collisions to take place are elastic and the surfaces are frictionless. Show that the motions of the two blocks are periodic. Find the time period of these periodic motions. Neglect the widths of the blocks.
The period of oscillation of a body of mass m1 suspended from a light spring is T. When a body of mass m2 is tied to the first body and the system is made to oscillate, the period is 2T. Compare the masses m1 and m2
A 20 cm wide thin circular disc of mass 200 g is suspended to rigid support from a thin metallic string. By holding the rim of the disc, the string is twisted through 60° and released. It now performs angular oscillations of period 1 second. Calculate the maximum restoring torque generated in the string under undamped conditions. (π3 ≈ 31)
Find the number of oscillations performed per minute by a magnet is vibrating in the plane of a uniform field of 1.6 × 10-5 Wb/m2. The magnet has a moment of inertia 3 × 10-6 kg/m2 and magnetic moment 3 A m2.
Which of the following example represent periodic motion?
A swimmer completing one (return) trip from one bank of a river to the other and back.
Which of the following example represent periodic motion?
A freely suspended bar magnet displaced from its N-S direction and released.
Which of the following example represent periodic motion?
A hydrogen molecule rotating about its center of mass.
A simple pendulum of frequency n falls freely under gravity from a certain height from the ground level. Its frequency of oscillation.
The equation of motion of a particle is x = a cos (αt)2. The motion is ______.
The displacement time graph of a particle executing S.H.M. is shown in figure. Which of the following statement is/are true?
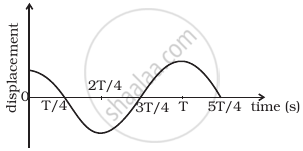
- The force is zero at `t = (T)/4`.
- The acceleration is maximum at `t = (4T)/4`.
- The velocity is maximum at `t = T/4`.
- The P.E. is equal to K.E. of oscillation at `t = T/2`.
