Advertisements
Advertisements
Question
The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 m. If the piston moves with simple harmonic motion with an angular frequency of 200 rad/min, what is its maximum speed?
Solution 1
Stroke of piston = 2 times the amplitude
Let A = amplitude,stroke = 1 m
`:. => A = 1/2 m`
Angular frequency, ` omega = 200 "rad/min"`
`V_"max" = ?`
We know that the maximum speed of the block when the amplitude is A
`V_"max" = omegaA = 200 xx 1/2 = 100 "m.min"`
`= 100/60 = 5/3 ms6(-1)= 1.67 ms^(-1)`
Solution 2
Angular frequency of the piston, ω = 200 rad/ min.
Stroke = 1.0 m
Amplitude, `A = 1.0/ 2= 0.5 m`
The maximum speed (vmax) of the piston is give by the relation:
`V_"max" = Aomega`
`= 200 xx 0.5 = 100 "m/min"`
APPEARS IN
RELATED QUESTIONS
Answer in brief:
Derive an expression for the period of motion of a simple pendulum. On which factors does it depend?
The total mechanical energy of a spring-mass system in simple harmonic motion is \[E = \frac{1}{2}m \omega^2 A^2 .\] Suppose the oscillating particle is replaced by another particle of double the mass while the amplitude A remains the same. The new mechanical energy will
Two bodies A and B of equal mass are suspended from two separate massless springs of spring constant k1 and k2 respectively. If the bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of A to that of B is
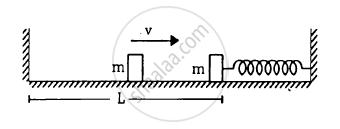
The left block in figure moves at a speed v towards the right block placed in equilibrium. All collisions to take place are elastic and the surfaces are frictionless. Show that the motions of the two blocks are periodic. Find the time period of these periodic motions. Neglect the widths of the blocks.
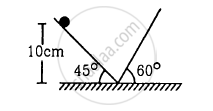
Find the time period of the motion of the particle shown in figure . Neglect the small effect of the bend near the bottom.
A uniform plate of mass M stays horizontally and symmetrically on two wheels rotating in opposite direction in Figure . The separation between the wheels is L. The friction coefficient between each wheel and the plate is μ. Find the time period of oscillation of the plate if it is slightly displaced along its length and released.

Find the time period of small oscillations of the following systems. (a) A metre stick suspended through the 20 cm mark. (b) A ring of mass m and radius r suspended through a point on its periphery. (c) A uniform square plate of edge a suspended through a corner. (d) A uniform disc of mass m and radius r suspended through a point r/2 away from the centre.
Find the number of oscillations performed per minute by a magnet is vibrating in the plane of a uniform field of 1.6 × 10-5 Wb/m2. The magnet has a moment of inertia 3 × 10-6 kg/m2 and magnetic moment 3 A m2.
Which of the following example represent periodic motion?
A hydrogen molecule rotating about its center of mass.
When two displacements represented by y1 = a sin(ωt) and y2 = b cos(ωt) are superimposed the motion is ______.
