Advertisements
Advertisements
प्रश्न
Displacement versus time curve for a particle executing S.H.M. is shown in figure. Identify the points marked at which (i) velocity of the oscillator is zero, (ii) speed of the oscillator is maximum.

उत्तर
In SHM y-t graph, zero displacement values correspond to the mean position; where the velocity of the oscillator is maximum.
Whereas the crest and troughs represent extreme positions, where displacement is maximum and velocity of the oscillator is minimum and is zero. Hence,
- A, C, E and G are either crests or trough having zero velocity.
- Speed is maximum at mean positions represented by B, D, F, and H paints.
APPEARS IN
संबंधित प्रश्न
A particle having mass 10 g oscillates according to the equation x = (2.0 cm) sin [(100 s−1)t + π/6]. Find (a) the amplitude, the time period and the spring constant. (c) the position, the velocity and the acceleration at t = 0.
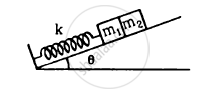
The block of mass m1 shown in figure is fastened to the spring and the block of mass m2 is placed against it. (a) Find the compression of the spring in the equilibrium position. (b) The blocks are pushed a further distance (2/k) (m1 + m2)g sin θ against the spring and released. Find the position where the two blocks separate. (c) What is the common speed of blocks at the time of separation?
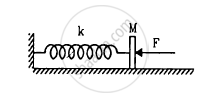
In following figure k = 100 N/m M = 1 kg and F = 10 N.
- Find the compression of the spring in the equilibrium position.
- A sharp blow by some external agent imparts a speed of 2 m/s to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.
- Find the time period of the resulting simple harmonic motion.
- Find the amplitude.
- Write the potential energy of the spring when the block is at the left extreme.
- Write the potential energy of the spring when the block is at the right extreme.
The answer of b, e and f are different. Explain why this does not violate the principle of conservation of energy.
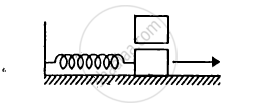
The springs shown in the figure are all unstretched in the beginning when a man starts pulling the block. The man exerts a constant force F on the block. Find the amplitude and the frequency of the motion of the block.
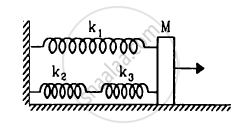
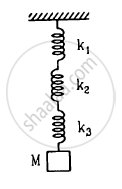
Find the elastic potential energy stored in each spring shown in figure, when the block is in equilibrium. Also find the time period of vertical oscillation of the block.
A 1 kg block is executing simple harmonic motion of amplitude 0.1 m on a smooth horizontal surface under the restoring force of a spring of spring constant 100 N/m. A block of mass 3 kg is gently placed on it at the instant it passes through the mean position. Assuming that the two blocks move together, find the frequency and the amplitude of the motion.
Find the elastic potential energy stored in each spring shown in figure when the block is in equilibrium. Also find the time period of vertical oscillation of the block.
When a particle executing S.H.M oscillates with a frequency v, then the kinetic energy of the particle?
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
The total energy of a particle, executing simple harmonic motion is ______.
where x is the displacement from the mean position, hence total energy is independent of x.
