Advertisements
Advertisements
प्रश्न
A tunnel is dug through the centre of the Earth. Show that a body of mass ‘m’ when dropped from rest from one end of the tunnel will execute simple harmonic motion.
उत्तर
Consider the situation shown in the diagram.
The gravitational force on the particle at a distance r from the centre of the earth arises entirely from that portion of matter of the earth in shells internal to the position of the particle. The external shells exert no force on the particle.
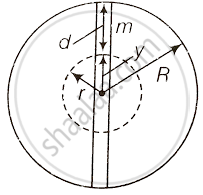
More clearly,
Let g' be the acceleration at P.
So, `g^' = g(1 - d/R) = g((R - d)/R)`
From the figure, `R - d = y`
⇒ `g^' = g y/R^'`
Force on the body at p,
F = `- mg^' = (- mg)/R y` .......(i)
⇒ F ∝ – y ......[Where y is the distance from the centre]
So, motion is S.H.M.
For time period, we can write equation (i)
As ma = `- (Mg)/Ry`
⇒ `a = - g/R y`
Comparing with a = `- ω^2y`
`ω^2 = g/R`
⇒ `((2pi)/T) = g/R`
⇒ T = `2pi sqrt(R/g)`
APPEARS IN
संबंधित प्रश्न
The period of a conical pendulum in terms of its length (l), semi-vertical angle (θ) and acceleration due to gravity (g) is:
A spring having with a spring constant 1200 N m–1 is mounted on a horizontal table as shown in Fig. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.

Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
Answer the following questions:
The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than `2pisqrt(1/g)` Think of a qualitative argument to appreciate this result.
A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t = 0. Determine the amplitude of the resulting oscillations in terms of the parameters ω, x0 and v0. [Hint: Start with the equation x = acos (ωt+θ) and note that the initial velocity is negative.]
Show that, under certain conditions, simple pendulum performs the linear simple harmonic motion.
A simple pendulum has a time period of T1 when on the earth's surface and T2 when taken to a height R above the earth's surface, where R is the radius of the earth. The value of `"T"_2 // "T"_1` is ______.
Which of the following statements is/are true for a simple harmonic oscillator?
- Force acting is directly proportional to displacement from the mean position and opposite to it.
- Motion is periodic.
- Acceleration of the oscillator is constant.
- The velocity is periodic.
When will the motion of a simple pendulum be simple harmonic?
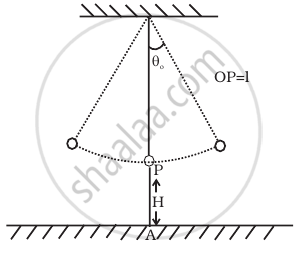
A simple pendulum of time period 1s and length l is hung from a fixed support at O, such that the bob is at a distance H vertically above A on the ground (Figure). The amplitude is θ0. The string snaps at θ = θ0/2. Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume θo to be small so that sin θo = θo and cos θo = 1.
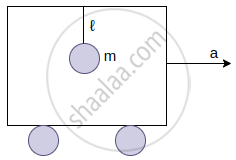
A pendulum of mass m and length ℓ is suspended from the ceiling of a trolley which has a constant acceleration a in the horizontal direction as shown in the figure. Work done by the tension is ______.
(In the frame of the trolley)