Advertisements
Advertisements
Question
पाँच त्रिभुज खींचिए और उनकी भुजाओं को मापिए। प्रत्येक स्थिति में जाँच कीजिए कि किन्हीं दो भुजाओं की लंबाईओं का योग तीसरी भुजा की लंबाई से सदैव बड़ा है।
Solution
केस 1. आइए हम एक त्रिभुज ABC बनाएँ
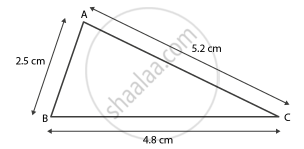
AB = 2.5 सेमी
BC = 4.8 सेमी और
AC = 5.2 सेमी
AB + BC = 2.5 सेमी + 4.8 सेमी
= 7.3 सेमी
7.3 > 5.2 के रूप में
∴ AB + BC > AC
इस प्रकार, हम देखते हैं कि त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा से अधिक होता है।
केस 2. आइए हम एक त्रिभुज PQR बनाएं
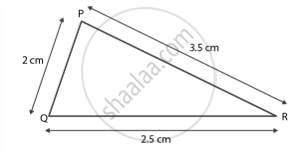
PQ = 2 सेमी
QR = 2.5 सेमी
PR = 3.5 सेमी
PQ + QR = 2 सेमी + 2.5 सेमी
= 4.5 सेमी
4.5 > 3.5 के रूप में
∴ PQ + QR > PR
इस प्रकार, हम देखते हैं कि त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा से अधिक होता है।
केस 3. आइये हम एक त्रिभुज XYZ बनाते
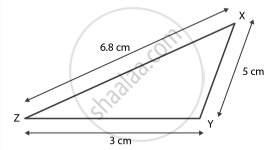
XY = 5 सेमी
YZ = 3 सेमी
ZX = 6.8 सेमी
XY + YZ = 5 सेमी + 3 सेमी
= 8 सेमी
8 > 6.8 के रूप में
∴ XY + YZ > ZX
इस प्रकार, हम देखते हैं कि त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा से अधिक होता है।
केस 4. आइए हम एक त्रिभुज MNS बनाएं
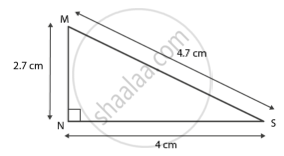
MN = 2.7 सेमी
NS = 4 सेमी
MS = 4.7 सेमी
MN + NS = 2.7 सेमी + 4 सेमी
6.7 सेमी
6.7 > 4.7 के रूप में
∴ MN + NS > MS
इस प्रकार, हम देखते हैं कि त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा से अधिक होता है।
केस 5. आइए हम एक त्रिभुज KLM बनाएं
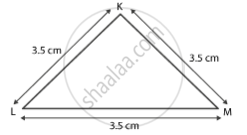
KL = 3.5 सेमी
LM = 3.5 सेमी
KM = 3.5 सेमी
KL + LM = 3.5 सेमी + 3.5 सेमी
= 7 सेमी
जैसे 7 सेमी > 3.5 सेमी
∴ KL + LM > KM
इस प्रकार, हम देखते हैं कि त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा से अधिक होता है।
इसलिए हम यह निष्कर्ष निकालते हैं कि त्रिभुज की किन्हीं दो भुजाओं का योग सदैव तीसरी भुजा से अधिक होता है।
APPEARS IN
RELATED QUESTIONS
निम्नलिखित त्रिभुज का प्रकार लिखिए:
त्रिभुज जिसकी भुजाएँ 7 सेमी, 8 सेमी और 9 सेमी हैं।
निम्नलिखित त्रिभुज का प्रकार लिखिए:
∆DEF जिसमें m∠D = 90° हैं।
निम्नलिखित त्रिभुज का प्रकार लिखिए:
ΔXYZ जिसमें m∠Y = 90° और XY = YZ हैं।
निम्नलिखित त्रिभुज का प्रकार लिखिए:
ΔLMN जिसमें m∠L = 30°, m∠M = 70° और m∠N = 80° हैं।
निम्नलिखित त्रिभुज का दो प्रकार से नामकरण कीजिए (आप कोण का प्रकार केवल देखकर ज्ञात कर सकते हैं।)

निम्नलिखित त्रिभुज का दो प्रकार से नामकरण कीजिए (आप कोण का प्रकार केवल देखकर ज्ञात कर सकते हैं।)
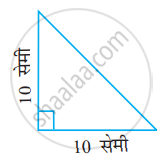
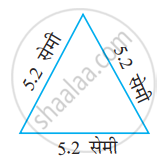
निम्नलिखित त्रिभुज का दो प्रकार से नामकरण कीजिए (आप कोण का प्रकार केवल देखकर ज्ञात कर सकते हैं।)
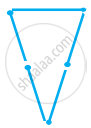
माचिस की तीलियों की सहायता से त्रिभुज बनाने का प्रयत्न कीजिए। इनमें से कुछ आकृति में दिखाए गए हैं।
 |
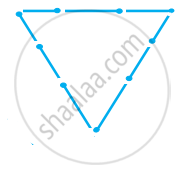 |
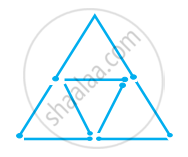 |
क्या आप 4 माचिस की तीलियों से एक त्रिभुज बना सकते हैं?
(ध्यान रखिए की आपको प्रत्येक स्थिति में सभी उपलब्ध माचिस की तीलियों का उपयोग करना है)। प्रत्येक स्थिति में त्रिभुज के प्रकार का नाम बताइए। यदि आप त्रिभुज नहीं बना पाते हैं, तो उसके कारण के बारे में सोचिए।
बहुभुज का नाम लिखिए।

दो और उदाहरण बनाइए।
एक सम षड्भुज (regular hexagon) का एक रफ़ चित्र खींचिए। उसके किसी तीन शीर्षों को जोड़कर एक त्रिभुज बनाइए। पहचानिए कि आपने किस प्रकार का त्रिभुज खींचा है।
