Question

Parikshit makes a cuboid of plasticine of sides 5cm, 2cm, 5cm. How many such cuboids will he need to form a cube?

Answer 1

Here, some cuboids of size 5 × 2 × 5 are given.

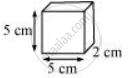
When these cuboids are arranged to form a cube, the side of this cube so formed will be a common multiple of the sides (i.e., 5, 2, and 5) of the given cuboid.

LCM of 5, 2, and 5 = 10

Let us try to make a cube with a 10 cm side.

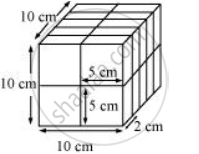
For this arrangement, we have to put 2 cuboids along with its length, 5 along with its width, and 2 along with its height.

Total cuboids required according to this arrangement: 2 × 5 × 2 = 20

With the help of 20 cuboids of such measures, a cube is formed as follows:

Alternatively

Volume of the cube on sides: 5cm, 2cm, 5cm

= 5cm × 2cm × 5cm = (5 × 5 × 2) cm³

Here, two 5s and one 2 are left that are not in a triplet.

If we multiply this expression by 2 × 2 × 5 = 20, then it will become a perfect cube.

Thus, (5 × 5 × 2 × 2 × 2 × 5) = (5 × 5 × 5 × 2 × 2 × 2) = 1000 is a perfect cube.

Hence, 20 cuboids of 5cm, 2cm, and 5cm are required to form a cube.