Question

ΔPQR की रचना इस प्रकार करें कि `angle`Q = 70°, `angle`R = 80° तथा PQ + QR + PR = 9.5 सेमी।

Answer 1

कच्ची आकृति:

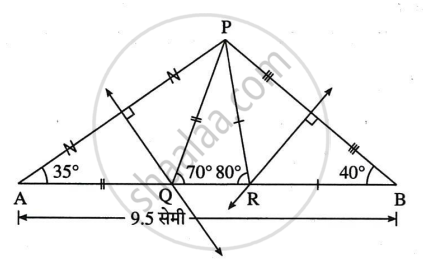
स्पष्टीकरण:

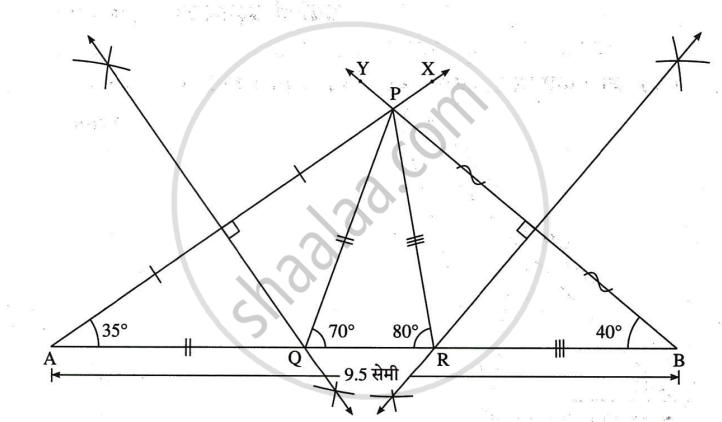
इस आकृति में रेख QR पर बिंदु A तथा B इस प्रकार लीजिए कि AQ = PQ, RB = PR

∴ AB = AQ + QR + RB = PQ + QR + PR = 9.5 सेमी

अब ΔAQP में AQ = QP

∴ `angle`PAQ = `angle`APQ तथा `angle`PAQ + `angle`APQ = बहिष्कोण PQR = 70°. . . . (दूरस्थ अंतःकोण प्रमेय से)

`angle`PAQ = `angle`APQ = 35° इसी प्रकार `angle`RBP = `angle`RPB = 40°

अब हम ΔAPB की रचना कर सकते हैं।

क्योंकि इस त्रिभुज के दो कोण तथा उसमे समाविष्ट भुजा AB ज्ञात है।

∴ QP = QA

∴ बिंदु Q के रेख PA के लंबसमद्‌विभाजक पर स्थित है तथा RP = RB

∴ बिंदु R रेख PB को लंबसमद्‌विभाजक पर स्थित है रेख PA तथा रेख PB के लंबसमद्‌विभाजक खींचें।

दोनो समद्‌विभाजक में रेख AB को जिन बिंदुओं पर प्रतिच्छेदित करती है वहाँ क्रमशः बिंदु Q तथा बिंदु R प्राप्त होते हैं।

रचना के सोपान

1. 9.5 सेमी लंबाई वाला रेखाखंड AB खींचिए।
2. बिंदु A से 35° माप का कोण बनाने वाली किरण खींचिए।
3. बिंदु B से 40° माप का कोण बनाने वाली किरण खींचिए।
4. दोनों किरणों के प्रतिच्छेदन बिंदु को P नाम दीजिए।
5. रेख PA तथा रेख PB के लंबसमद्‌विभाजक खींचिए । वे रेखा AB को जिन बिंदुओं पर प्रतिच्छेदित करते हैं उन्हें क्रमशः Q और R नाम दीजिए।
6. रेख PQ और रेख PR खींचिए।

ΔPQR यह अभीष्ट त्रिभुज है।