Advertisements
Advertisements
Question
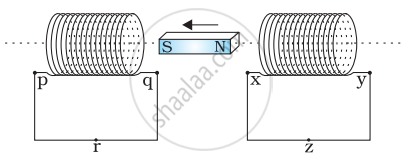
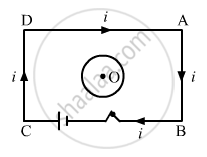
Predict the direction of induced current in the situation described by the following figure.
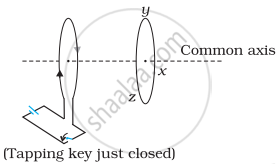
Solution
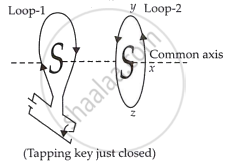
Lenz's law specifies the direction of the induced current in a closed loop. Using Lenz’s rule, the direction of the induced current in the given situation can be predicted as follows:
As the current increases, the inner side of loop-1 becomes the south pole. Consequently, the loop's inside should Lenz claim that it will also turn into the south pole law.
The direction of the induced current is along yzxy.
APPEARS IN
RELATED QUESTIONS
State Lenz's law. Illustrate, by giving an example, how this law helps in predicting the direction of the current in a loop in the presence of a changing magnetic flux.
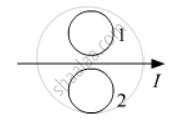
What is the direction of induced currents in metal rings 1 and 2 when current I in the wire is increasing steadily?
Show that Lenz's law is a consequence of conservation of energy.
Consider the situation shown in figure. If the closed loop is completely enclosed in the circuit containing the switch, the closed loop will show _______________ .
Explain, with the help of a suitable example, how we can show that Lenz's law is a consequence of the principle of conservation of energy.
A conducting wire XY of mass m and neglibile resistance slides smoothly on two parallel conducting wires as shown in figure. The closed circuit has a resistance R due to AC. AB and CD are perfect conductors. There is a ˆ. magnetic field `B = B(t)hatk`.
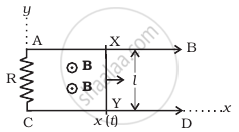
- Write down equation for the acceleration of the wire XY.
- If B is independent of time, obtain v(t) , assuming v(0) = u0.
- For (b), show that the decrease in kinetic energy of XY equals the heat lost in R.
A metallic ring of mass m and radius `l` (ring being horizontal) is falling under gravity in a region having a magnetic field. If z is the vertical direction, the z-component of magnetic field is Bz = Bo (1 + λz). If R is the resistance of the ring and if the ring falls with a velocity v, find the energy lost in the resistance. If the ring has reached a constant velocity, use the conservation of energy to determine v in terms of m, B, λ and acceleration due to gravity g.
Predict the direction of induced current in the situation described by the following figure.