Question

Prove that the bisector of the vertex angle of an isosceles triangle bisects the base perpendicularly.

Answer 1

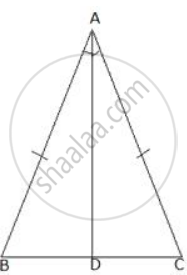
In ΔADB and ΔADC
AB = AC  ...(given)
AD = AD ...(common)
∠BAD = ∠CAD  ...(AD bisects ∠BAC)
Therefore, ΔADB ≅ ΔADC
Hence, BD = Dc and ∠BDA = ∠CDA
But ∠BDA + ∠CDA = 180°
⇒ ∠BDA = ∠CDA = 90°
Therefore, AD bisects BC perpendicularly.