Advertisements
Advertisements
Question
In the figure ΔABC is isosceles with AB = AC. Prove that:
∠A : ∠B = 1 : 3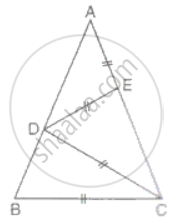
Sum
Solution
In ΔDEC,
∠DEC = ∠ADE + ∠A = 2a ...(ext. Angle to ΔADE)
DE = DC
⇒ ∠DEC = ∠DCE = 2a .........(ii)
In ΔBDC, let ∠B = b
DC = BC
⇒ ∠BDC = ∠B = b .........(iii)
In ΔABC,
∠ADB =∠ADE + ∠EDC + ∠BDC
180 = a + ∠EDC + b (from (i) and (ii))
∠EDC = 180° - a - b .......(iv)
Now again in ΔDEC
180° = ∠EDC + ∠DCE + ∠DEC ...(from (ii))
180° =∠EDC + 2a + 2a
∠EDC = 180° - 4a
Equality (iv) and (v)
180° - a - b = 180° - 4a
3a = b .....(vi)
`"a"/"b" = (1)/(3) = (∠"A")/(∠"B")`
Hence, ∠A : ∠B = 1 : 3.
shaalaa.com
Is there an error in this question or solution?
