Advertisements
Advertisements
Question
Rain is falling vertically with a speed of 30 m s–1. A woman rides a bicycle with a speed of 10 m s–1in the north to south direction. What is the direction in which she should hold her umbrella?
Solution 1
The described situation is shown in the given figure.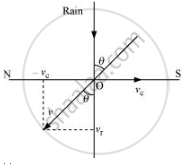
Here,
vc = Velocity of the cyclist
vr = Velocity of falling rain
In order to protect herself from the rain, the woman must hold her umbrella in the direction of the relative velocity (v) of the rain with respect to the woman.
`vecv = vec(v_r) + (-vecv_c)`
Resultant, |v| = `sqrt(v_(r^2)+ v_(c^2))`
|v| = `sqrt(30^2+10^2)`
|v| = `sqrt(900+100)`
|v| = `sqrt1000 = 10sqrt10m`
`tan theta = v_c/v_r = 10/30`
`theta = tan^(-1)(1/3)`
`theta = tan^(-1)(0.333) ~~18^@`
Hence, the woman must hold the umbrella toward the south, at an angle of nearly 18° with the vertical
Solution 2
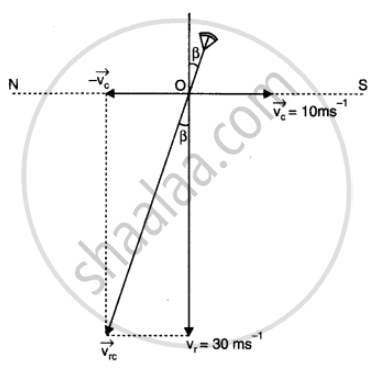
The situation has been demonstrated in the figure below. Here `vecv = 30 "ms"^(-1)` is the rain velocity in vertically downward direction and `vecv_c = 10 ms^(-1)` is the velocity of cyclist women in horizontal plane from north N to south S.
∴Relative velocity of rain w.r,t cyclist `vecv_(rc)` subtends an angle β with verticle such that
`tan beta = |vecv_c|/|vecv_r| = 10/30 = 1/3`
`:. beta = tan^(-1)(1/3) - 18^@26`
Hence the woman should hold her umberlla at `18^@26` south of verticle
APPEARS IN
RELATED QUESTIONS
A fighter plane flying horizontally at an altitude of 1.5 km with speed 720 km/h passes directly overhead an anti-aircraft gun. At what angle from the vertical should the gun be fired for the shell with muzzle speed 600 m s–1 to hit the plane? At what minimum altitude should the pilot fly the plane to avoid being hit? (Take g = 10 m s–2).
A ship A is moving Westwards with a speed of 10 km h–1 and a ship B which is at 100 km South of A, is moving Northwards with a speed of 10 km h–1. The time after which the distance between them becomes shortest, is
Suppose that two objects A and B are moving with velocities `vec("V"_"A")` and `vec("V"_"B")` (each with respect to some common frame of reference). Let `vec("V"_"AB")` represents the velocity of A with respect to B then:
A swimmer wants to cross a river from point A to point B. Line AB makes an angle of 30° with the flow of river. Magnitude of velocity of the swimmer is same as that of the river. The angle θ with the line AB should be ______°, so that the swimmer reaches point B.
A clock has a continuously moving second's hand of 0.1 m length. The average acceleration of the tip of the hand (in units of ms-2) is of the order of ______.
