Advertisements
Advertisements
Question
Ray PQ and ray PR are perpendicular to each other. Points B and A are in the interior and exterior of ∠QPR respectively. Ray PB and ray PA are perpendicular to each other. Draw a figure showing all these rays and write -
- A pair of complementary angles
- A pair of supplementary angles.
- A pair of congruent angles.
Sum
Solution
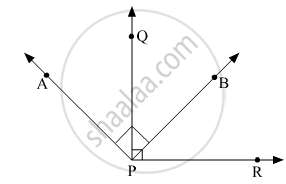
Since ray PQ ⊥ ray PR, then m∠QPR = 90∘ and ray PA ⊥ ray PB, then m∠APB = 90∘.
(i) Two angles, sum of whose measures is 90∘, are called complementary angles.
Here, m∠QPR = 90∘
⇒ m∠BPQ + m∠BPR = 90∘
∴ ∠BPQ and ∠BPR are complementary angles.
(ii) Two angles, sum of whose measures is 180∘, are called supplementary angles.
⇒ m∠APB + m∠QPR
= 90∘ + 90∘
= 180∘
∴ ∠APB and ∠QPR are supplementary angles.
(iii) Angles with the same measures are called congruent angles.
Here, m∠QPR = m∠APB = 90∘
∴ ∠APB and ∠QPR are congruent angles.
shaalaa.com
Use of properties of parallel lines
Is there an error in this question or solution?