Advertisements
Advertisements
Question
Prove that, if a line is perpendicular to one of the two parallel lines, then it is perpendicular to the other line also.
Solution
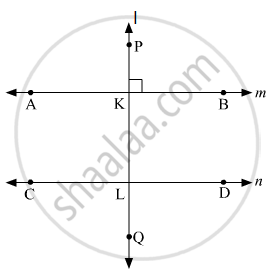
Suppose m and n are two parallel lines and line l is their transversal. Suppose line l ⊥ line m.
Let us mark the points A and B on line m, C and D on line n and P and Q on line l.
Suppose the line l intersects line m and line n at K and L respectively.
Since, line l ⊥ line m, then ∠PKB = 90∘.
Since, line AB || line CD and transversal PQ intersects them at K and L respectively, then
∠KLD = ∠PKB ...(Corresponding angles)
⇒ ∠KLD = 90∘
∴ line l ⊥ line n.
APPEARS IN
RELATED QUESTIONS
In ΔABC, ∠A = 76°, ∠B = 48°, ∴ C = ______.
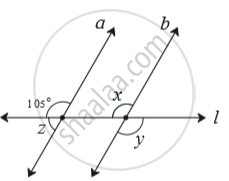
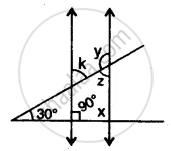
In the adjoining figure, line a || line b. line l is a transversal. Find the measures of ∠x, ∠y, ∠z using the given information.
In the given figure, the directed lines are parallel to each other. Find the unknown angles.
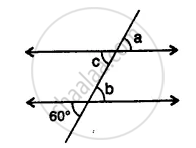
In the given figure, the directed lines are parallel to each other. Find the unknown angles.
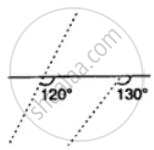
Which pair of the dotted line, segments, in the following figure, are parallel. Give reason:
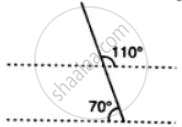
Which pair of the dotted line, segments, in the following figure, are parallel. Give reason:
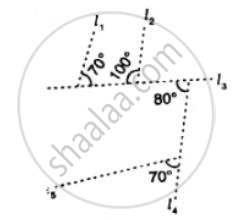
Which pair of the dotted line, segments, in the following figure, are parallel. Give reason:
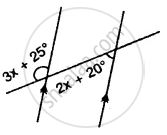
Find x, y and p is the given figure
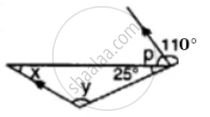
Find x in the following case:
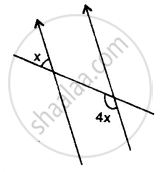
Find x in the following case: