Advertisements
Advertisements
Question
Represent graphically the displacement of 45 cm, 30° north of east
Solution
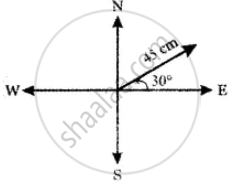
APPEARS IN
RELATED QUESTIONS
If `bara and barb` are any two non-zero and non-collinear vectors then prove that any vector `barr` coplanar with `bara` and `barb` can be uniquely expressed as `barr = t_1bara + t_2barb` , where t1 and t2 are scalars.
Represent graphically the displacement of 80 km, 60° south of west
A line makes angles α, β, γ with the co-ordinate axes and α + β = 90°, then γ = ______.
If C is the midpoint of AB and P is any point outside AB, then ______
If `overline (a) =10hat("i") + lambda hat("j") + 2hat("k")` is perpendicular to `overline (b)= hat ("i")+hat("j")-hat("k")`, then λ is equal to ______.
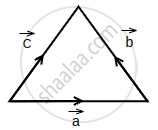
If `veca + vecb = vecc ((λx)hati + yhatj + 4zhatk) + (yhati + xhatj + 3yhatk) = -zhati - 2zhatj - (λ + 1)xhatk` are sides of triangle as shown is figure then value of λ is ______.
(where x, y, z are not all zero)
If a = `veca = hati + hatj - 2hatk, vecb = 2hati - hatj + hatk` and `vecc = 3hati - hatk` and `vecc = mveca + nvecb`, then m + n is equal to ______.
Let a = `hati + 2hatj + hatk`, b = `hati - hatj + hatk`, c = `hati + hatj - hatk`. A vector coplanar to a and b has a projection along with c of magnitude `1/sqrt(3)`, then the vector is ______.
The position vectors of vertices of ΔABC are `4hati - 2hatj; hati + 4hatj - 3hatk` and `-hati + 5hatj + hatk` respectively, then ∠ABC = ______.
In the triangle PQR, `bar("PQ") = 2bar "a"` and `bar("QR") = 2bar "b".` The mid-point of PR is M. Find the following vectors in terms of `bar "a" "and" bar"b"`.
In the triangle PQR, `\overline"PQ"` = 2`\overline"a"` and `\overline"QR"` = 2`\overline"b"`. The mid-point of PR is M. Find the following vectors in terms of `\overline"a"` and `\overline "b"`.
- `\overline"PR"`
- `\overline"PM"`
- `\overline"QM"`
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk, "and" 3hati + 4hatk` form a triangle or not.
In the triangle PQR, `bar(PQ)` = 2 `bara` and `bar(QR)` = 2 `barb`. The mid-point of PR is M. Find the following vectors in terms of `bara` and `barb`.
- `bar(PR)`
- `bar(PM)`
- `bar(QM)`
Check whether the vectors `2hati + 2hatj+3hatk,-3hati+3hatj+2hatk` and `3hati+4hatk` form a triangle or not.
