Advertisements
Advertisements
Question
Resistances R1, R2, R3 and R4 are connected as shown in the figure. S1 and S2 are two keys. Discuss the current flowing in the circuit in the following cases.
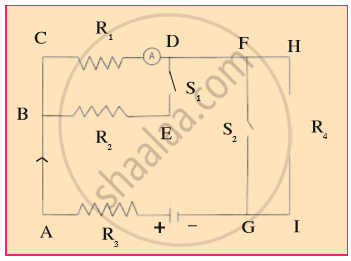
- Both S1 and S2 are closed.
- Both S1 and S2 are open.
- S1 is closed but S2 is open.
Solution
a.
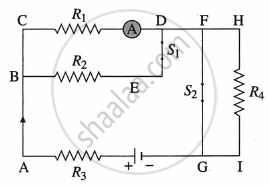
Due to zero resistance of FG in parallel series combination of R4, the resultant resistance of this combination will also be almost zero and the entire electric current will flow through the PQ path.
Resultant resistance of parallel series combination of R1, R2
∴ `"I"_3 = "V"/("R"_3 + "R"_S)`
`"V"_1 = "V" - "I"_3"R"_3`
= `"V" - ("R"_3"V")/("R"_3 + "R"_"p")`
= `"V"(1 - "R"_3/("R"_3 + "R"_"p"))`
= `"V"("R"_"p"/("R"_3 + "R"_"p"))`
∴ `"I"_1 = "V"_1/"R"_1 = "V"/"R"_1("R"_"p"/("R"_3 + "R"_"p"))`
similarly,
`"I"_2 = "V"/"R"_2("R"_"p"/("R"_3 + "R"_"p"))`
b.
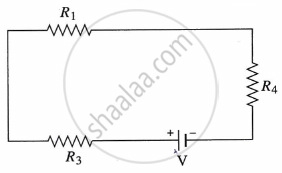
Equivalent resistance of series combination of R1, R3, R4
`"R"_"S" = "R"_1 + "R"_3 + "R"_4`
Current in the circuit,
`"I" = "V"/("R"_1 + "R"_3 + "R"_4)`
c.
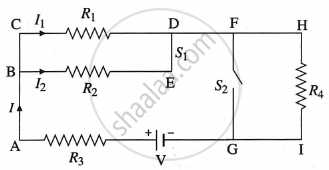
`"R"_"P" = ("R"_1"R"_2)/("R"_1 + "R"_2)`
`"R"_"S" = "R"_3 + "R"_4 + ("R"_1"R"_2)/("R"_1 + "R"_2)`
`"I" = "V"/"R"_"S" = "I"_3 = "I"_4`
Also, `"I" = "I"_1 + "I"_2 and "R"_1"I"_1 = "R"_2"I"_2`
∴ `"I" = "I"_1 + ("I"_1"R"_1)/"R"_2`
∴ `"I"_1(1 + "R"_1/"R"_2)`
= `("I"_1("R"_1 + "R"_2))/"R"_2`
`"I"_1 = ("R"_2"I")/("R"_1 + "R"_2)`
and `"I"_2 = ("I"_1"R"_1)/"R"_2`
= `"R"_1/"R"_2(("R"_1I)/("R"_1 + "R"_2))`
= `("R"_1I)/("R"_1 + "R"_2)`
APPEARS IN
RELATED QUESTIONS
Draw circuit symbols for
fixed resistance
Draw circuit symbols for
A closed switch
What is open circuit?
In the circuit diagram below, 10 units of electric charge move past point x every second What is the current in the circuit ______.
Draw the circuit diagram for the following series connection
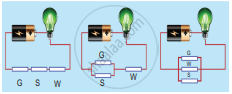
Study the three electric circuits below. Each of them has a glass rod (G), a steel rod (S), and a wooden rod (W).
In which of the electric circuits would the bulb not light up.
_____ has a thin metallic filament that melts and breaks the connection when the circuit is overheated.
State whether true or false. If false, correct the statement.
Ammeter is connected in parallel in any electric circuit.
When a circuit is open, _____ cannot pass through it.
A device that is used to break an electric circuit is called ______.
Instead of metal wires, a jute string can be used to make a circuit.
What are the types of electric circuits?
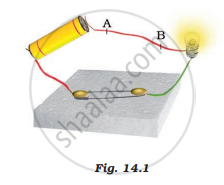
When an electric current flows through a copper wire AB as shown in Figure14.1, the wire
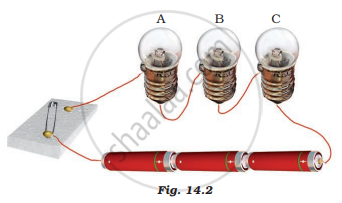
Three bulbs A, B, and C are connected in a circuit as shown in Figure 14.2. When the switch is ‘ON’

In the above circuit, if the current reading in the ammeter A is 2A, what would be the value of R1?
What are the essential components of an electric circuit?
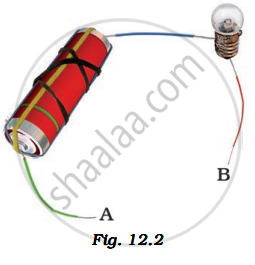
In the following arrangement shown in Fig. 12.2, the bulb will not glow if the ends A and B are connected with
How is Joule's law effect useful in electric circuits where fuse is used as a safety device?
