Advertisements
Advertisements
Question
Rewrite the following statement without using the connective ‘If ... then’.
If 10 − 3 = 7 then 10 × 3 ≠ 30.
Solution
Let p : 10 − 3 = 7
q : 10 × 3 ≠ 30
The given statement is p → q.
But p → q ≡ ~p ∨ q.
∴ The given statement can be written as
'10 - 3 ≠ 7 or 10 × 3 ≠ 30'.
APPEARS IN
RELATED QUESTIONS
Examine whether each of the following statement patterns is a tautology or a contradiction or a contingency.
[~(~p ∧ ~q)] v q
Evaluate: ∫ x . log x dx
Write converse, inverse contrapositive of the statement "If two triangles are not congruent then their areas are not equal.
Write the following compound statement symbolically.
The angle is right angle if and only if it is of measure 90°.
Construct the truth table of the following statement pattern.
(p ∧ q) ↔ (q ∨ r)
Construct the truth table of the following statement pattern.
(q → p) ∨ (∼ p ↔ q)
Construct the truth table of the following:
[(p ∧ q) ∨ r] ∧ [∼r ∨ (p ∧ q)]
Determine the truth values of p and q in the following case:
(p ∨ q) is T and (p ∧ q) is T
Determine the truth values of p and q in the following case:
(p ∨ q) is T and (p ∨ q) → q is F
Write the truth value of the following statement.
Earth is a planet and Moon is a star.
Write the truth value of the following statement.
16 is an even number and 8 is a perfect square.
Write the truth value of the following statement.
A quadratic equation has two distinct roots or 6 has three prime factors.
Write the negation of the following statement.
2 + 3 ≠ 5
Write the truth value of the negation of the following statement.
London is in England.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
Kavita is brilliant and brave.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
If Kiran drives the car, then Sameer will walk.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The drug is effective though it has side effects.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
If a real number is not rational, then it must be irrational.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
If the question paper is not easy then we shall not pass.
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
If proof is lengthy then it is interesting.
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
It is not true that the proof is lengthy but it is interesting.
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
(p ∧ q) ∨ r
Write the negation of the following.
If ∆ABC is not equilateral, then it is not equiangular.
Write the negation of the following.
Ramesh is intelligent and he is hard working.
Rewrite the following statement without using the connective ‘If ... then’.
If a quadrilateral is rhombus then it is not a square.
Write the negation of the following statement.
∃ x ∈ A, such that x + 5 < 11.
Without using truth table prove that:
~ (p ∨ q) ∨ (~ p ∧ q) ≡ ~ p
Write the following statements in symbolic form
Milk is white if and only if the sky is not blue
Write the following statements in symbolic form
If Kutab – Minar is in Delhi then Taj - Mahal is in Agra
Write the negation of p → q
State whether the following statement is True or False:
The converse of inverse of ~ p → q is q → ~ p
Write the following statements in symbolic form.
If Qutub – Minar is in Delhi then Taj-Mahal is in Agra
The symbolic form of the following circuit is (where p, q represents switches S1 and S2 closed respectively)
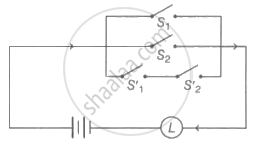
Which of the following is false?
Using the statements
p: Seema is fat,
q: Seema is happy,
Write the following statements in symbolic form;
- Seema is thin and happy.
- If Seema is fat then she is unhappy.
Write the negation of (p `leftrightarrow` q).
Construct the truth table for the statement pattern:
[(p → q) ∧ q] → p
